Suchen
01.04.2020
Treibstoffverbrauch in l/h oder l/km berechnen?
 Wenn man über die Verbräuche von Booten liest, stolpert man über Angaben in unterschiedlichen Bezugsystemen.
Wenn man über die Verbräuche von Booten liest, stolpert man über Angaben in unterschiedlichen Bezugsystemen.
So findet man Verbräuche in l/km bzw km/l (Kehrwert! 1/(l/km) ergibt km/l und vice versa) bzw. sm/l oder l/sm und auch angaben in l/h.
Was davon funktioniert aber nun besser für eine Reichweitenberechnung bezüglich eines Bootes?
Diese Frage lässt sich mit einer simplen Beispielrechnung sehr einfach beantworten.
Für diese Rechnung nehmen wir mal “einfache” Werte, die aber nahe an der Wahrheit liegen.
Wir gehen mal von einer Strecke von 150km aus - das wäre in meinem Anwendungsfall Helgoland und zurück (2×75km).
Als Geschwindigkeit für normales Wetter legen wir mal rund 50km/h fest.
Mit 50km/h brauchen wir nun für die 150km 3h (150km:50km/h=3h).
Der Motor konsumiert nun angenommen 0,5 l/km ; das macht auf 150km 75l Gesamtverbrauch.
Umgerechnet wären das 75l/3h= 25 l/h.
Bis hierhin ist alles realistisch.
Änderung der Bedingungen:
Nun kommt aber Wind auf und die Wellen werden höher und steiler.
Wir reduzieren die Geschwindigkeit auf unterste Gleitfahrt; sagen wir 25km/h.
Was passiert? Der Motor konsumiert nun nicht mehr 0,5 l/km sondern durch das Bremsen in den Wellen und den dadurch verlängerten Weg erhöht sich der Verbrauch ein wenig. Allerdings wird der Verbrauch andererseits durch die Drehzahlanpassung und die kleinere
Geschwindigkeit gesenkt. Unterm Strich tut sich in der Realität wenig, denn wir sind ja noch gleitend unterwegs.
Wir können weiterhin von rund 0,55 l/km ausgehen, was bedeuten würde: 150kmx0,55 l/km= 82,5l. Wir benötigen also nun 7,5l mehr für die gesamte Strecke.
Rechnen wir das mal in l/h:
Die Geschwindigkeit halbiert sich, daher sind wir nun statt der 3h für die gleche Distanz 6h auf dem Wasser.
Ausgehend von nun 25 l/h wären wir bei 6hx25 l/h= 150 Liter.
Das wäre ja fast mein gesamter Tankinhalt.
Kann das trotz Gleitfahrt möglich sein? Natürlich nicht.
Rechnen mit dem maximalen Verbrauch als Gegenprobe:
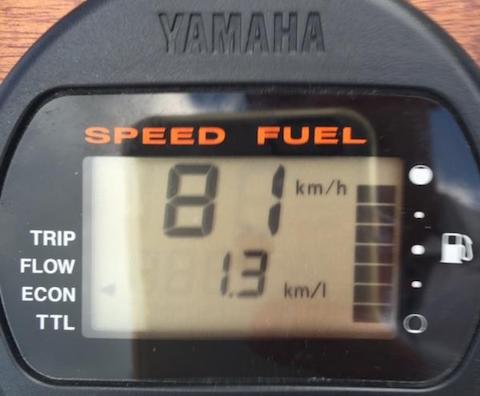
Laut meinem Foto kommt mein Boot bei 81km/h noch gut 1,3km mit einem Liter weit.
1/1,3 - also der Kehrwert - ergibt den Verbrauch in l/km: 0,769l l/km.
Würde ich also die Strecke mit Vollgas fahren, würde das bedeuten ich verbrauche insgesamt 150kmx0,769 l/km= 115,4 Liter!
Also selbst bei Vollgas und dem daraus resultierenden maximalen Verbrauch würde ich noch weit von den 150 Litern, die wir mit der Methode der Reichweitenberechnung in Litern/Stunde errechnet haben, entfernt sein.
Erfahrungen:
Tatsächlich ist es in der Realität so, dass die SeaQuest bei optimalen Bedingungen 0,417 Liter/km konsumiert:
Selbst mit 50 km/h liegt sie noch um 0,45 l/km. Der Maximale Verbrauch den ich bei schwerer See um 6-7 Windstärken gegen die See im Halbgleiten jemals gemessen habe liegt um 0.55 l/km bzw. 1,8km/l.
Das bedeutet in der Praxis für meine Berechnungen:
Ich kann für jede Tour bei Normalwetter von 0,5 l/km ausgehen und habe dabei bereits konservativ gerechnet. Es bildet sich eine kleine Reserve, da ich die 0,5 l/km nicht ganz brauche.
Ist höherer Seegang angekündigt, rechne ich mit 0,6 l/km im absoluten Maximum.
Damit komme ich in der Realität bis Windstärke 7 immer aus. Etwaige Abweichungen durch den Mehrverbrauch beim Starten oder zeitweisem Halbgleiten rechnen sich mit dem Rein- und Raustuckern aus Zonen mit Geschwindigkeits-beschränkung erfahrungsgemäß sehr gut gegen.
Wenn ich in Verdrängerfahrt unterwegs bin, was bei schwerer See sehr komfortabel funktioniert, bleibe ich sogar unter 0,38 l/km.
Rechnet das eingangs beschriebene Szenario mal für 10km/h Verdrängerfahrt in l/h durch. Da wären wir bei 375 l, wobei in der Realität keine 75 l verbraucht würden.
Leerlauf und langsame Rumpfgeschwindigkeit:
Bis die normale Fahrt in Marschgeschwindigkeit erreicht ist,
hat man oftmals schon 20-30 Minuten lang den Motor laufen- denn man hat abgelegt, die Leinen verstaut, die Fender eingeholt und ist in Rumpfgeschwindigkeit aus dem Hafen getuckert bis man dann in einem Gebiet ist, in welchem schnelles Gleiten zulässig ist .
Selbiges Szenario ergibt sich erneut beim Einlaufen in den nächsten Hafen.
In dieser Stunde hat man aber keine 25l verbraucht, sondern in der Realität ist man vielleicht 2-3km gefahren und hat (0,3 l/km x 3km =) 0,9L konsumiert. Auch hier liegt die Rechnung nach Litern/km wieder deutlich näher an der Wahrheit - denn selbst wenn wir mit 0,5 l/km rechnen würden läge das Ergebnis bei 1,5 l (3kmx0,5 l/km) für diese Stunde.
Kann man diese kurzen Abschnitte in Rumpfgeschwindigkeit denn nicht vernachlässigen?
Hier ein ganz typisches Beispiel eines Motorprotokolls:
5.Data Logger [Engine operating hours according to engine speed],,,,,,,,,,,,,,,,
Engine speed,,,,,,,,,,,,,,,,
- 1000 r/min,,,,,, 169.9,,,,,,,,,,
1000 - 2000 r/min,,,,,, 168.4,,,,,,,,,,
2000 - 3000 r/min,,,,,, 57.2,,,,,,,,,,
3000 - 4000 r/min,,,,,, 63.7,,,,,,,,,,
4000 - 5000 r/min,,,,,, 4.6,,,,,,,,,,
5000 - 6000 r/min,,,,,, 0.0,,,,,,,,,,
6000 - 7000 r/min,,,,,, 0.0,,,,,,,,,,
Total operating hours,,,,,, 463,,,,,,,,,,
Der Motor ist also insgesamt 463 Stunden lang gelaufen, davon 170 Stunden mit unter 1000 Umdrehungen - also Standgas oder Leerlauf.
Das sind rund 37% Standgas oder Leerlauf - Weitere 37% bewegen sich bei 1000-2000 r/min! Ein großer Anteil daran sind Strecken mit Geschwindigkeitsbegrenzung oder geht zum Manövrieren drauf. Bei fast jedem Motor finden sich ähnliche Werte und das ist wirklich völlig normal. Lest Eure Motoren einfach mal aus; Ihr werdet erstaunt sein.
Um die Frage zu beantworten: Nein, gerade diese Abschnitte mit geringer Drehzahl machen Zeitlich einen großen Anteil jeder Tour aus - und verfälschen damit die Berechnung in l/h extrem.
Passt es denn bei gleichbleibendem Wetter, aber unterschiedlichen Geschwindigkeiten?
Wie man sieht, ist mein Verbrauch bei 40 km/h kaum anders als der bei 53 km/h.
Wir rechnen weiter mit unseren 0,5 l/km als Faustwert, die Abweichung ist ja gering (siehe Fotos weiter oben)
Mit der Zeit als Basis aber gäbe es selbst hier bei ganz glatter See ein großes Delta:
Bei 40 km/h würde man 3,75h unterwegs sein, bei 53km/h wäre man hingegen nur 2,85h auf dem Wasser. Man wäre also ein Viertel schneller, denn 2,85 ist fast exakt 75% von 3,75:
40km/h -> 2,85hx25 l/h= 71,25L ….das ist realistisch, zu 40 km/h passt die Angabe in l/h.
52km/h -> 3,75hx25 l/h= 93,75L ….Das wären über 22l mehr! Passt also überhaupt nicht.
Die Angaben l/h ändern sich also drastisch mit der Änderung der Zeitbasis.
Wir stellen also fest:
Sobald man also von den normalen Fahrparametern bei Schönwetter nur ganz geringfügig abweicht, läuft jede Berechnung auf Basis von Litern/Stunde komplett aus dem Ruder.
Mit einem Wert in l/h lässt sich auch für einen potentiellen Käufer überhaupt nicht einschätzen, was das Boot ihn in der Zukunft kosten wird.
Meine persönliche Erfahrung ist, dass so ziemlich alle Verbräuche die man mir jemals in l/h für Boote genannt hat umgerechnet auf den Kilometer absolut unrealistisch erscheinen.
Wer mit solchen Werten um sich wirft, weiß entweder nicht was sein Boot verbraucht oder
möchte nicht wirklich damit herausrücken.
Mit einer Berechnung bei der die Distanz die Basis darstellt können wir sehr genau rechnen, egal ob es nun l/km oder l/sm sind, und wir haben immer eine recht genaue Vorstellung davon, für welche Strecke der Treibstoff im Tank noch ausreicht.
Frank - 10:44 @ Seemannschaft | 56 Kommentare
-
Chrischan
Bei der Reichweitenberechnung in l/h bei “gerade noch Gleitfahrt” hast du meiner Meinung nach einen Denkfehler.
Wenn du davon ausgehst, dass das Boot 0,55 L/km braucht, sind das bei 150 km = 82,5 L Sprit.
Soweit klar.
Du gehst dann aber plötzlich wieder von 25 L/h aus der 50km/h Berechnung aus.
Du fährst aber ja nur 25 km/h und brauchst dabei 82,5 l für 6 Stunden Fahrt = 13,75 L / Stunde, was auch viel realistischer ist. Der Motor braucht schließlich weniger Kratfstoff, weil noch in Gleitfahrt, aber deutlich langsamer.Somit sind auch Angabe in L/h nicht so realitätsfern, wie du oben angemerkt hast.
Grüße!
-
Frank
Chrischan, das was Du als Denkfehler betrachtest ist meine Argumentation in der ich darlege, warum sich in l/h nicht rechnen lässt.
Was verbraucht der Motor denn jetzt? Die 25l/h bei 50 km/h oder die 13,75l/h bei 25 km/h?
Die 25l/h habe ich bei 25 km/h angenommen um zu beweisen, wie unsinnig die Berechnung in l/h ist. Als Berechnungsgrundlage benötigt man einen Wert, der sich möglichst wenig ändert.
Wenn Du in l/km oder l/sm rechnest kannst Du von einem relativ konstanten Wert ausgehen und damit lässt sich immer sehr zuverlässig planen - auch wetterunabhängig. -
Puuh
Du hast Recht: Verbrauchswerte in Liter pro km oder umgekehrt in km pro Liter sind realistischer als reine Liter pro Stunde Angaben. Besonders bei einem Gleiter, der ja oft in verschiedenen Geschwindigkeiten fährt, wobei dann jeweils andere Werte für L/h zum Tragen kommen.
Bei Verdrängern sieht das anders aus. Diese fahren meist mit ziemlich konstanter Geschwindigkeit (so etwa zwischen 10 und 12 km/h). Dabei ist der Verbrauch in L/h ziemlich konstant und deswegen auch als ein gängiger Vergleichswert für Verdränger geeignet.
Aber ist Dir in deiner Rechnung nicht doch ein Fehler unterlaufen? Schau nochmal in deine letzte Beispielrechnung.
Da schreibst du, bei 40 km/h brauchst du für die Strecke 3,75 Stunden; und bei 50 km/h sind es 2,85 Stunden.
In deiner Rechnung sieht das aber anders aus:
Zitat
40km/h -> 2,85hx25 l/h= 71,25L ….das ist realistisch, zu 40 km/h passt die Angabe in l/h.
52km/h -> 3,75hx25 l/h= 93,75L ….Das wären über 22l mehr! Passt also überhaupt nicht.
Zitat Ende.
Also, da hast du wohl die beiden Zeiten vertauscht. Bzw. die Geschwindigkeiten zu Beginn der Zeilen.
Außerdem rechnest du bei beiden Geschwindigkeiten mit dem gleichen Verbrauch pro Stunde, nämlich mit 25l/h, was ja ebenfalls nicht ganz der Realität entsprechen dürfte.PS: Aber Dein Blog gefällt mir! Und Dein Boot ist ebenfalls Klasse. Gratulation dazu!
Gruß
Volker
(Puuh aus dem boote-forum) -
buy cheap generic cialis online
Howdy this is kind of of off topic but I was wanting
to know if blogs use WYSIWYG editors or if you have to manually code
with HTML. I’m starting a blog soon but have no coding knowledge so I
wanted to get advice from someone with experience.
Any help would be enormously appreciated! -
daily cialis online
First off I would like to say superb blog!
I had a quick question which I’d like to ask if you do not mind.
I was curious to know how you center yourself and clear your head before writing.
I’ve had trouble clearing my thoughts in getting my thoughts out there.
I do enjoy writing but it just seems like the first 10 to 15
minutes tend to be lost just trying to figure out how to begin. Any recommendations or tips?
Thanks! -
sungarments.Com
1’400 Patienten, welche die Hb/Hkt WHO Kriterien für PV erfüllt haben, identifiziert.
Mit der Entdeckung von JAK2-Treibermutationen im Jahr 2005 und
breit verfügbaren Methoden zur Testung stellt
die PV meist keine diagnostische Schwierigkeit mehr dar. Eine diagnostische Herausforderung ist dagegen die JAK2-unmutierte d.h.
JAK-2 unfavorable Polyzythämie, welche eine heterogene Gruppe von Entitäten umfasst.
Produziert der Körper nicht genügend Testosteron, kann eine
Substitutionstherapie mit natürlichem Testosteron erfolgen.
Unser vorgeschlagener Diagnosealgorithmus für
JAK2-unmutierte Polyzythämie bei Erwachsenen ist in Abbildung 1 dargestellt.Zusammenfassend kann gesagt werden, dass die Polyzythämie und Erythrozytose wichtige Laborbefunde sind, welche eine weitere Abklärung triggern sollten. Parameter, die für die Kategorisierung dieser Artwork
von Polyzythämie wegweisend sind, umfassen den Epo-Spiegel im Serum und den P50-Wert.Im Hoden spielt Testosteron eine wesentliche Rolle bei der
Spermatogenese. Über diese androgene Wirkung hinaus werden Sexualverhalten und
-aktivität beim Mann beeinflusst. Dementsprechend vielgestaltig ist
die klinische Ausprägung eines Testosteronmangels. Die Substitutionsbehandlung mit Testosteronpräparaten ist in der Praxis
fest etabliert. Therapienutzen und Risiken müssen jedoch je
nach Indikation sorgfältig abgewogen werden.
Durch eine homozygote Mutation des VHL-Gens entsteht ein VHL-Protein mit reduzierter
Aktivität, sodass die a-Ketten auch bei Normoxämie nicht abgebaut werden. Die
dadurch hervorgerufene Erhöhung der Erythropoietin-Ausschüttung führt zu
einem deutlichen Anstieg des Hämoglobinwertes.Dies weist auf andere Ursachen, wie zum Beispiel die beobachtete vermehrte Produktion des vaskulären endothelialen Wachstumsfaktors (VEGF),
die ebenfalls durch HIF reguliert wird, hin (3). Angeborene Erythropoietin(EPO)-Rezeptor-Mutationen führen zu einer Verkürzung des intrazellulären Anteils des Rezeptorproteins
(2). Dadurch können negative Regulatoren nicht mehr binden, sodass es zu einer konstitutiven Aktivierung des Rezeptors kommt.
Im Gegensatz zur PV haben die Betroffenen kein erhöhtes Risiko für Thrombosen und Blutungen, was dafür spricht, dass die
Erythrozytose nicht alleine dafür verantwortlich ist. Während die Menopause mit dem Ausbleiben der Regelblutung offensichtlich wird, fehlt ein solches Kardinalereignis
beim Mann.
Beispiele hierfür sind der Wilms-Tumor, polyzystische Nieren, Nierenzellkarzinome und die Posttransplantationserythrozytose.
Die Gabe von Erythropoietin, beispielsweise zur Behandlung der Tumor- oder renalen Anämie, führt zu einem Erythrozytenanstieg.
Auf welchen Wert das Hämoglobin angehoben werden soll,
wird derzeit diskutiert, weil eine zu starke Stimulierung in einzelnen Studien eine sinkende Überlebensrate zeigte (5).
Verschiedene, mit Zyanose einhergehende Herzfehler (zum Beispiel Septumdefekte,
Links-Rechts-Shunt) führen zu chronischer Hypoxämie und damit über eine Erythropoietin-Erhöhung zu einer kompensatorischen Erythrozytose.Die PV ist eine hämatologische, klonale Erkrankung, welche zu der Gruppe der
myeloproliferativen Neoplasien (MPN) gehört. Die PV-Patienten haben ein deutlich erhöhtes Risiko für venöse
und arterielle thromboembolische (auch lebensbedrohliche) Ereignisse.
Zudem besteht bei ihnen ein Risiko für die Entwicklung einer Myelofibrose, einer Kind der MPN mit einer ungünstigeren Prognose.
In seltenen Fällen kann die Erkrankung auch in eine akute myeloische Leukämie (AML) fortschreiten. Gemäss der Klassifikation der Tumorerkrankungen der Weltgesundheitsorganisation (WHO)
sowie dem Internationalen Consensus der Klassifikation (ICC) der MPN aus dem Jahr 2022 gibt es klare diagnostische
Kriterien für die PV (Tab. 1). Prostatakrebszellen sind in der Lage,
das Hormon Testosteron für ihr eigenes Wachstum zu nutzen. Durch Hormonentzug kann es vorübergehend
zu einem Stillstand des Tumorwachstums kommen.
Auf den Einsatz zytoreduktiver Medikamente mit
leukämogenem Risikoprofil sollte insbesondere bei jungen Patienten verzichtet werden. Das 20-Jahres-Risiko eines Übergangs in eine
postpolyzythämische Myelofibrose, das heißt eine Verfaserung des Knochenmarks mit zunehmender Auswanderung der
Hämatopoese in Milz und Leber, betrug in der Studie 10
% (12). Da die angeborenen Polyzythämien und die sekundäre Polyzythämie bei zyanotischen kongenitalen Herzerkrankungen selten hämatologische Behandlung
erfordern, wird im Folgenden nur die Therapie der PV dargestellt.
Ziel ist es, die PV-assoziierten potenziell lebensbedrohlichen thromboembolischen und Blutungskomplikationen sowie die auftretenden unspezifischen Symptome zu mindern.
Ursache der Testosteron-bedingten Polyglobulie ist vermutlich eine gehemmte
Ausschüttung von Hepcidin, das an der Regulation des Eisenstoffwechsels beteiligt ist.
Aus ungeklärten Gründen erhöht sich außerdem die Erythropoetin-Freisetzung.
Es gibt auch Berichte über eine vermehrte inflammatorische Aktivität unter Testosteron-Substitution – dies könnte eine
Erklärung für die beobachtete Leukozytose des Patienten sein. Zunächst jedoch behandelten die Schweizer Internisten den Patienten auf Grundlage
der erhobenen Informationen wie einen Polycythaemia-Patienten. Er erhielt zur Thrombozytenaggregationshemmung
Clopidogrel und wurde mehrfach zur Ader gelassen. -
https://cambodiaexpertalliance.net/employer/can-you-measure-testosterone/
It is possible that you may have heard some horror tales concerning
withdrawal symptoms from stopping testosterone substitute therapy,
or that critical unwanted effects can occur once
you cease taking testosterone. Most of these stories are rumors, and the outcomes of misinformation, and people
who have misused or abused testosterone. It is true that your
physique can have withdrawal-like symptoms when you cease taking testosterone.Nevertheless, such negative impacts of stopping testosterone almost all the time occur if you
stop all of a sudden, without your doctor’s authorization.
It is not a good idea underneath any circumstances to
stop “cold turkey.” If you feel you’re experiencing unwanted side effects, or
not getting the outcomes you need, from your testosterone
therapy, do not simply cease. Monitoring hormone ranges helps make
positive that the testosterone dose is suitable for your needs.It is important to note that testosterone levels should be monitored regularly via blood tests to ensure optimum hormone ranges and
to detect any potential unwanted side effects
or complications. These blood tests could also be carried
out every few months or as advised by the healthcare skilled.
Starting with a lower dose is widespread follow, as it allows the healthcare skilled to monitor the individual’s response
to the remedy and regulate the dose accordingly.It is essential to remember that the aim of hormone substitute therapy is to realize and keep hormone ranges inside the normal vary for
cisgender males. Most healthcare professionals advocate starting with
a weekly injection schedule to rapidly establish steady hormone ranges.After a couple of weeks, the frequency may be adjusted
primarily based on the individual’s response to remedy and blood take a look at results.The dosage and administration of testosterone will
differ depending on your individual wants.
Hudson’s Information has been around since 2004 and is the one
resource I continue to return to. I extremely recommend
it for further analysis into the alternative ways testosterone could be administered and why individuals select a method of administering it
over the opposite, among different things.
Many people think about transition—especially medical transition—as a means of going from
level A to point B. I’m non-binary, though, and I can let you know that that’s not always how transition goes.A healthcare provider will contemplate any underlying medical situations,
corresponding to coronary heart illness or liver problems, which
can have an effect on the metabolism and clearance of testosterone from the physique.Individuals with certain medical conditions may require lower dosages
or extra frequent injections. Testosterone injections are commonly
used to treat conditions similar to low testosterone ranges, certain kinds of most cancers, and delayed puberty.
The frequency of testosterone injections can range depending on several factors, including the individual’s specific needs and the type
of testosterone getting used. It is crucial to keep in thoughts that each particular person’s journey
and response to testosterone therapy will be
unique. Working carefully with a knowledgeable healthcare professional
will guarantee the very best outcomes and minimize potential risks.If you aren’t seeing the adjustments you need on GAHT, talk together
with your clinician. Half of that conversation would possibly include what gender-affirming surgical options might off to
satisfy your specific targets. To reduce danger, the goal for people
taking masculinizing hormone remedy is to keep hormone levels within the vary that’s typical for cisgender males — males whose gender identity aligns
with their sex assigned at birth. Masculinizing hormone remedy is used to make bodily modifications in the physique that are brought on by male hormones throughout puberty.
This hormone therapy might help higher align the physique with an individual’s gender identity.
Masculinizing hormone therapy also is called gender-affirming hormone therapy.If you’re a individual assigned feminine at delivery (AFAB)
and are considering transitioning to male, testosterone therapy,
commonly known as hormone replacement remedy (HRT), could also be an important part of your
journey. Testosterone remedy may help you develop male secondary sexual characteristics, similar to
facial hair growth and a deeper voice. However, before starting testosterone therapy, you will need to perceive the
rules and protocols for a protected and profitable transition.
Some individuals might select to complement their testosterone levels via medical remedies, such as testosterone alternative therapy (TRT).However, it is important to understand that there can be potential unwanted effects
of taking testosterone at a selected frequency. Testosterone remedy can have unwanted side
effects and potential dangers that must be monitored carefully.
Some widespread side effects embrace zits, oily pores and skin, elevated physique
hair growth, and changes in mood or libido. Additionally, long-term testosterone use could improve the risk of certain health circumstances, corresponding to heart problems and liver issues.Your doctor can suggest one of the best remedy options on your low testosterone
levels and your alcohol dependence. Mixing steroids and alcohol can create a cycle of
dependence on each substances with out the individual being conscious of
it. Gender-affirming hormone therapy is an effective and secure short-termtreatment in Thai transgender men. Apart from the standard advice,uric acid, plasma glucose,
and creatinine level evaluation before and duringmasculinizing hormone remedy are rational practices.
An intramusculartestosterone enanthate 250 mg each four weeks is
another masculinizingregimen with decent efficacy and security
profile. This web page incorporates details about testosterone, a hormone
used for hormone alternative remedy (HRT). -
Buylegalsteroids.Com
Not only are they loaded with anti-inflammatory compounds, but additionally they have potential
testosterone-boosting brokers similar to quercetin. This precursor converts
to a mild androgen that increases sexual attractiveness to
ladies. Not instantly testosterone, however is a built-in primordial
trait in man.
Fermented foods like yogurt and kimchi can not directly assist testosterone ranges by ensuring your gut microbiota is wholesome.
A healthy gut plays a role in inflammation and hormone metabolism, so eating gut-friendly meals is all the time
good. While way of life changes like moderating alcohol and quitting smoking are needed for
maintaining testosterone ranges, one other necessary factor
is what you eat. These are the highest meals to add to
your food plan if you need to elevate your testosterone ranges to a wholesome vary.
Testosterone boosters, also known as test boosters,
declare to assist improve testosterone levels.If you imagine you’re poor in magnesium, contemplate having some amaranth- you’ll be glad you
did as quickly as you find out that it’s additionally a whole and rich supply of protein. It is the primary male intercourse hormone and
performs an enormous function, together with its metabolite DHT, in making you a man. Excessive dose zinc dietary supplements appear to be effective for treating hypogonadism in some males, but zinc supplements usually are not presently
recommended as a common treatment for hypogonadism (22).One of the most important vitamins that can assist increase testosterone ranges is vitamin D3.
In 2011, the outcomes of a research published in the journal Hormone and Metabolic Research discovered that vitamin D supplementation boosts
testosterone naturally in overweight men by as a lot as 30 %.Studies conclude that magnesium consumption is linked to increased
testosterone levels among male athletes.
The significance of supplements is hotly debated, however
finally, your health is dependent upon the right quantities
of nutrients that you simply absorb. Studies present that testosterone remedy can enhance sexual performance (7).
You can have roasted pumpkin seeds as a pleasant night snack.Reeder pointed to zinc, vitamin D, magnesium, omega-3 fatty acids and high-quality protein as pivotal vitamins for wholesome testosterone manufacturing.
Things that elevate testosterone ranges embrace regular
exercise (especially weightlifting), getting sufficient
sleep, managing stress, and eating a balanced
diet wealthy in zinc and vitamin D. By supporting lower cortisol levels, cordyceps mushrooms can cut back oxidative stress,
fight fatigue, and assist naturally balance your testosterone ranges.
Since this ‘shroom just isn’t readily available in our diets, it’s usually taken in complement type.
Before you go foraging for it within the forest, it’s another ingredient
we’ve included in our Testosterone System.
Our Strawberry-Banana Green Smoothie is made with flaxseed, allowing for a simple way to embrace this dietary powerhouse in your food regimen. Age
is a significant determinant of testosterone ranges, notes StatPearls.
After predominantly being produced in the testes or the ovaries in, testosterone circulates within the blood where the hormone has an effect on various systems within the physique.You’re probably most acquainted with testosterone as the
intercourse hormone answerable for defining “manhood.” And sure, it does.
Maintaining the proper degree of testosterone may be challenging.
Wholesome girls make up to 300 micrograms of testosterone in their ovaries and adrenal glands every day.
Our staff aims to be not solely thorough with its research, but also goal and unbiased.
Magnesium, a mineral present in spinach and darkish, leafy greens, blocks
certain proteins from binding with testosterone. -
Ezworkers.Com
70918248
-
vagyonor.hu
Diese können laut Healthline den Hormonhaushalt durcheinanderbringen. Zudem
haben Studien gezeigt, dass ein übermäßiger Alkoholkonsum ebenfalls unfavorable Auswirkungen auf das beste Testosteron hat – dein Schlüssel zu
mehr Energie und besserer Gesundheit. Stell dir vor, du
bist auf einer Reise, die dein Leben verändern wird.Du hast bereits den ersten Schritt gemacht und erfahren, wie
bestimmte Lebensmittel deinen Testosteronspiegel steigern können.
Sechs bis acht Stunden Schlaf pro Nacht sind best, um die Testosteronbildung zu fördern. Wenn du
deinen Stress reduzierst, kann sich dies positiv auf deinen Testosteronspiegel auswirken. Durch
die Reduzierung des Stresslevels kann der Spiegel des Hormons im
Körper ansteigen und es entsteht mehr Energie und Lebenslust.
Eine Studie an älteren Männern ergab, dass jene mit mehr als 7 Stunden Schlaf pro Nacht einen höheren Testosteronspiegel hatten als
diejenigen mit weniger als 7 Stunden.
Zusätzlich kann eben die Frau noch ▷ Femmax ennehmen, für den Mann eignet sich wie schon erwähnt ▷ Viacinil.Männer brauchen ihre Libido, ihren Antrieb, um die Frau zu umwerben. Deswegen spricht auch der Mann in 99%
der Fälle die Frau an, nicht andersrum. Testosteron ist das Hormon, was uns antreibt – sowohl Mann als auch Frau.Stress ist nicht nur für deine allgemeine Gesundheit schädlich, sondern kann auch einen direkten Einfluss auf deinen Testosteronspiegel haben. Der Hauptgrund
dafür ist die Produktion des Stresshormons Cortisol, das
in direktem Zusammenhang mit Testosteron steht. Mit diesen Lebensmitteln kannst du nicht nur deinen Testosteron natürlich steigern,
sondern auch deinen allgemeinen Gesundheitszustand verbessern. Mit diesen kannst du schnell und effektiv dein Testosteron natürlich steigern. Mit Mitte 20 hatte ich für ganze 2 Jahre mit
Potenzproblemen zu kämpfen… Bis ich nach unzähligen Arztbesuchen und Selbstexperimenten endlich herausfand, was wirklich hilft.Regelmäßiges Krafttraining, insbesondere mit hoher Intensität, kann die Testosteronproduktion steigern. Eine ausgewogene Ernährung mit ausreichender Zufuhr von Zink und Vitamin D ist ebenfalls entscheidend.
Zusätzlich wurde beobachtet, dass ausreichend
Schlaf und die Vermeidung von chronischem Stress die Hormonproduktion unterstützen.
Eine Phase-4-Studie, das TRAVERSE Trial, hat zudem gezeigt, dass Testosterontherapie bei Männern mit Hypogonadismus
keine erhöhten kardiovaskulären Risiken birgt. Dies muss dann zunächst ausgeglichen werden, was entweder
zu einem erhöhten oder zu niedrigen Testosteronspiegel führen kann.
Auch hier ist eine gesunde Ernährung mit guten Fetten wieder essenziell,
um den Körper zu unterstützen. Testosteron ist ein wichtiges Hormon für die Gesundheit und das
Wohlbefinden von Männern.
Lassen Sie uns die unglaublichen gesundheitlichen Vorteile von Hafer erkunden, darunter,
wie Hafer die Herzgesundheit verbessern, die Verdauung unterstützen und sogar bei der Gewichtskontrolle helfen kann.
Wenn Sie die gesamte Bandbreite der Vorteile von Haferflocken kennen, können Sie erkennen, warum es eine kluge Entscheidung ist, Hafer in Ihre Ernährung aufzunehmen. Testosteron spielt eine entscheidende Rolle für die Herz-Kreislauf-Gesundheit.Es kann die Produktion roter Blutkörperchen unterstützen, die für die Herzgesundheit unerlässlich ist.
Der Testosteronspiegel bestimmt Ihre sexuelle Kraft und nimmt nach dem
30. Neben diesem Rückgang gibt es auch einen Rückgang in anderen Bereichen. Ein niedriger Testosteronspiegel ist
zu einem solchen Downside geworden, dass etwa forty % der Männer über 45 davon betroffen sind.
Daneben hilft ein forderndes Exercise mit hohen Gewichten auch, Ihre Testosteronspeicher randvoll zu füllen.
Da in den Wintermonaten die Sonne weniger scheint und sich die meisten Menschen weniger an der frischen Luft aufhalten. Deswegen macht es an dieser Stelle Sinn Vitamin D über Nahrungsergänzungsmittel zu sich zu nehmen, sodass
Du weiterhin einen hohen Testosteronspiegel hast.Weiterhin geht mit einem hohen Vitamin-D-Spiegel auch ein hoher Testosteronspiegel einher.
Deswegen solltest Du dafür sorgen, dass Du ausreichend Vitamin D über die Sonne und die Nahrung zu Dir nimmst.Letzteres gilt übrigens nicht nur für Männer, sondern gleichermassen für Frauen. Frauen verfügen jedoch über wesentlich geringere Mengen dieses Hormons als Männer.
Das Wissen um diesen Effekt kann das Abnehmen deutlich erleichtern. Rauchen wiederum steht
in Verbindung mit einem niedrigeren Testosteronspiegel,
wobei die enthaltenen Chemikalien und der Tabakkonsum die Hodenfunktion beeinträchtigen können. Das ist einer der effektivsten Wege, um deinen Körper
schnell an seine Grenzen zu bringen, was die Testosteronproduktion steigert.
Einer der wichtigsten Faktoren, wenn du deinen Testosteronspiegel steigern möchtest, ist Bewegung. -
https://Edujoinnow.com/
Zum Beispiel verzeichnete John, ein 52-jähriger Patient aus
Glasgow mit Lebererkrankung, schwere, niedrige Testosteron-Symptome, die später mit
seiner Lebererkrankung verbunden waren. Sein Fall betont die Notwendigkeit einer umfassenden medizinischen Bewertung, wenn Symptome auftreten. Ein niedriger Testosteronspiegel (auch bekannt als Hypogonadismus oder niedriger T) ist ein ungewöhnlich
niedriger Testosteronspiegel im Blut. Es ist ein Androgen oder männliches Sexualhormon, das von Geburt an vorhanden ist und einen Fötus männlich macht.
Laut der Cleveland Clinic gibt es neben dem Altern viele andere Ursachen für einen verminderten Testosteronspiegel.Außerdem wirst du einer körperlichen Untersuchung und einer Anamnese unterzogen. Wenn dein Arzt davon überzeugt ist, dass du einen niedrigen Testosteronwert hast,
wirst du an einen Spezialisten überwiesen, der entweder Endokrinologe oder Urologe ist.
Nachdem du nun die verschiedenen Anzeichen und Symptome eines niedrigen Testosteronspiegels bei Männern kennst, möchtest
du bestimmt wissen, was die Ursache für einen Testosteronmangel ist.
Dies ist auch der Grund, warum ein niedriger Testosteronspiegel dein Risiko für Herzerkrankungen erhöht.
Niedrige Testosteron-Werte können zu ernsthaften Gesundheitsproblemen führen,
weshalb es für die meisten Männer wichtig ist,
einen Testosteronmangel zu beheben, um eine optimale Gesundheit zu gewährleisten.
Bei einer bestehenden Schilddrüsenerkrankung wird in regelmäßigen Abständen der Verlauf der Therapie überprüft.
T3 ist die Abkürzung für Trijodthyronin, das Schilddrüsenhormon mit drei Jodatomen, während T4 die Kurzversion für Thyroxin, das Hormon mit vier Jodatomen.
Man unterscheidet zwischen dem Anteil der Hormone, die an sogenannte Transporteiweiße gebunden sind
und den “freien” Hormonen, die im Blut frei zirkulieren.
Gemessen werden die Formen dieser Hormone – freies T3 (fT3)
und freies T4 (fT4) – da nur sie im Körper wirksam sind.
Auch starkes Übergewicht (Adipositas), akuter Schlafmangel,
Infekte oder Herzinsuffizienz können den TSH-Wert beeinflussen. Auch für die Verlaufskontrolle einer medikamentösen Behandlung ist
der TSH-Wert der wichtigste Indikator. Die Schilddrüse produziert lebenswichtige
Hormone, die entscheidende Körperfunktionen steuern – darunter das Herz-Kreislauf-System,
die Verdauung, den Knochenaufbau, das Nervensystem oder die Muskeln.
Krankheiten wie Diabetes, Nierenerkrankungen, COPD, Bluthochdruck
und Lebensstile wie Rauchen und Drogenmissbrauch tragen ebenfalls zu
einem niedrigen T-Wert bei. L-Thyroxin (Levothyroxin) ist ein künstlich hergestelltes Schilddrüsenhormon, das zur Behandlung einer Schilddrüsenunterfunktion eingesetzt wird.
Das im Körper wirksame Hormon ist das T3, das zahlreiche Stoffwechselvorgänge
beeinflusst.
Testosteron spielt eine Schlüsselrolle in einer Vielzahl von Körperfunktionen. Es beeinflusst nicht nur deine Muskelmasse und Knochendichte, sondern auch deine Stimmungslage.Es gibt durchaus einige Methoden, mit denen Sie Ihren Testosteronhaushalt aktivieren und im Gleichgewicht halten können. Am
besten funktionieren die gesunde Ernährung, körperliche Aktivität und
die Vermeidung von Stress.
Darüber hinaus kann eine frühzeitige Diagnose und Behandlung Muskel- und Knochenschwund verhindern. Viele der oben genannten Symptome können bei Frauen mit niedrigem T-Wert auftreten, mit Ausnahme der männlichen spezifischen Symptome.Ein Mangel an Vitamin B12 oder Folsäure führt zu
gestörter Zellteilung und vergrößerten, funktionsgestörten roten Blutkörperchen. Ursachen sind eine mangelhafte Ernährung, Aufnahmestörungen im Darm oder ein erhöhter Bedarf (z.
B. Schwangerschaft). Ein unbehandelter Vitamin-B12-Mangel kann Nervenschäden mit Kribbeln und
Taubheitsgefühlen verursachen.
Da Testosteron eine so wichtige Rolle im Körper eines Mannes spielt, wird ein niedriger Testosteronspiegel dein System aus dem Gleichgewicht bringen. Laut Studien speichern Männer
mit niedrigem Testosteronwerten mehr Fett in ihren Oberschenkeln als Männer mit normalem Testosteronspiegel.Dies ist einer der Gründe, warum niedrige Testosteronwerte und
ein Testosteronmangel von vielen Experten für männliche Osteoporose (Knochenschwund) verantwortlich gemacht wird.
Längere Fastenzeiten, die mehrere Tage dauern, können zu einem
niedrigen Testosteronspiegel führen. Gleichzeitig kann kurzes
intermittierendes Fasten Ihren niedrigen T-Wert tatsächlich verbessern. TRT steigert den Testosteronspiegel in einen normalen Bereich und
lindert so die Symptome eines niedrigen Testosteronspiegels.
Es gibt sie in verschiedenen Formen, wie transdermale
Gele, Injektionen und Pellets, jeweils mit spezifischen Anwendungsmethoden.
Fühlen Sie sich den ganzen Tag abgeschlagen und
fragen sich, warum Ihnen die Motivation fehlt und warum Sie auf gar nichts mehr Lust haben? Testosteron ist ein wichtiges
Hormon für Ihren Antrieb und die Motivation, alle
Herausforderungen im Privatleben und im Beruf zu meistern. Wird
es in minderer Menge gebildet, sind Müdigkeit und Abgeschlagenheit
trotz ausreichend Schlaf eine direkte Folge.
Die Schilddrüsenwerte informieren einerseits wie intestine
die Schilddrüse arbeitet und anderseits wie gut die
Interaktion in diesem Schilddrüsenregelkreis funktioniert.Ein niedriger Testosteronspiegel bei Frauen ist ein häufiges Drawback, von dem jedes Jahr mehr und mehr Frauen betroffen sind.
Immer mehr Frauen leiden unter den negativen Folgen eines klinisch niedrigen T-Werts.
Bevor Sie sich jedoch Sorgen machen, stehen Ihnen zahlreiche Behandlungen zur Verfügung, mit denen Sie das Drawback beheben können – und
bei den meisten geht es nur um Ihren Lebensstil.
Dies kann zu einer “Leiden in Stille” -Mentalität führen,
bei der Sie im schlimmsten Fall schauen und sich fühlen. Die Hauptursache für einen niedrigen Testosteronspiegel bei Frauen bei der oralen Pille ist, dass der SHBG-Spiegel
auf eine unkontrollierbare Konzentration erhöht wird.Aber die Wissenschaft sagt uns, dass es eine Reihe von häufigen Ursachen für einen niedrigen Testosteronspiegel gibt, die Sie beachten müssen.
-
how long can You be On steroids
The anticipation, arousal, and sexual need main as much as sexual exercise can even result in a temporary increase
in testosterone ranges. An earlier examine from 1992 assessed the effects
of sexual activity on testosterone levels in males and females.The researchers measured testosterone ranges earlier than and after intercourse
and in addition on days when there was no intercourse.
Researchers are excited about both the short-term and long-term effects of masturbation on testosterone levels.
Understanding the function of dopamine in sexual want can even make clear how varied
components, together with masturbation, may influence overall sexual
satisfaction and drive. This information may be significantly useful for individuals in search
of to optimize their sexual health and well-being.While frequent masturbation doesn’t appear to have a negative influence on testosterone ranges, sure lifestyle components can contribute to
low testosterone. These include persistent stress,
poor sleep, insufficient vitamin, lack of exercise, and obesity.
To assist wholesome testosterone levels, it is very
important concentrate on overall well-being and adopt a balanced life-style.
Another examine published within the journal Hormones and Habits looked at the effects of sexual activity, including masturbation, on testosterone ranges in both men and women. The research discovered that sexual exercise did not affect testosterone levels in both gender.
This further helps the notion that masturbation doesn’t have a big influence on testosterone manufacturing.The launch of testosterone throughout masturbation serves
a number of necessary functions. Firstly, it will increase blood
circulate to the genital space, making erections more frequent and sturdy in males.This hormone also enhances sensitivity and arousal, making the experience more gratifying and intense.
We source research from peer-reviewed medical journals, top authorities businesses,
leading academic institutions, and revered advocacy teams.We also go beyond the analysis, interviewing top consultants in their
fields to bring you the most knowledgeable insights.Additionally, you can find scientific research related to testosterone and well being at PubMed.
Let’s take a extra in-depth look at the science behind these myths and what analysis
really reveals about masturbation and testosterone ranges.
A research within the Archives of Sexual Behavior discovered that sexual activity led
to higher ranges of oxytocin and prolactin in comparison with masturbation. These differences spotlight the distinctive physiological
and psychological benefits of partnered sexual activity.A study printed in the Journal of Scientific Endocrinology & Metabolism found that males who engaged in common resistance coaching had larger testosterone
levels in comparability with sedentary people. This underscores the significance of bodily exercise in sustaining optimum
hormonal well being. However, with successful, non-hormonal
ED remedy resulting in resumption of sexual exercise, the study
individuals’ testosterone levels considerably increased.
These findings suggest that common sexual exercise — whether or
not solo or with a associate — helps preserve testosterone levels over time.Integrating masturbation into a healthy life-style can provide quite a few advantages, together
with stress aid and improved mood. As with any aspect of health, balance,
training, and self-awareness are essential.
It plays a vital function in various bodily capabilities similar
to muscle mass, bone density, sex drive, and mood regulation. Many males surprise if there is a correlation between masturbation and
testosterone levels, and if that is the case, how usually they want to engage on this activity to maintain up optimum ranges.Several studies have been performed to research the impression of ejaculation on testosterone levels.
One research printed within the “Journal of Endocrinology” examined the
hormonal modifications in men after sexual exercise. The researchers discovered
that testosterone levels have been elevated immediately after sexual
activity, but returned to baseline ranges inside a day.
This suggests that ejaculation results in a short lived enhance in testosterone ranges,
but these ranges normalize comparatively rapidly. These
findings recommend that refraining from masturbation for a certain period can actually boost testosterone ranges.Testosterone is a hormone that plays a vital position in numerous aspects of our well being,
corresponding to muscle and bone development, mood
regulation, and sexual function. Let’s delve into the
science behind it and discover this intriguing question. Testosterone
is a vital androgenic hormone primarily produced in males’s testes and,
to a lesser extent, in ladies’s ovaries. It plays a vital role in growing male reproductive tissues and maintaining
secondary sexual traits similar to muscle and bone mass,
as well as body hair.
Regular masturbation doesn’t lower testosterone levels or negatively affect hormone manufacturing.
It is also essential to emphasise that extreme masturbation can potentially lead to other
physical and psychological issues. For instance, people who have interaction in compulsive or addictive
masturbation may experience signs such as fatigue, decreased libido,
or difficulty achieving orgasm. These signs can contribute to emotions of
misery and can impact a person’s total high quality of life.
This means that sexual exercise, together with masturbation, may very well have a constructive affect on testosterone levels in males.
However, this increase in testosterone was not sustained beyond that interval.Smoking and ingesting extreme quantities of alcohol can affect
your T levels. One 2001 study of 10 adult males did discover that
refraining from masturbation for 3 weeks may trigger
a light enhance in T levels. Sexual activity,
including masturbation, can lead to the release of endorphins,
promoting leisure and stress reduction. -
https://jobs.ubuntu.education
Naturellement, ce cycle peut augmenter le degré d’effets secondaires (par rapport au protocole débutant).
Ainsi, la suppression de la testostérone est susceptible d’être accrue après le cycle ;
ainsi que la rétention d’eau/le risque de gyno, and so on. La
testostérone étant un stéroïde injectable, elle pénètre immédiatement dans la circulation sanguine ; ne fournissant
ainsi aucune contrainte évidente au foie. Une étude administrant
400 mg de testostérone orale par jour pendant 20 jours n’a présenté aucun effet indésirable sur les enzymes hépatiques.
Lorsque l’on entreprend un voyage pour améliorer sa silhouette et ses performances
athlétiques, il est crucial de comprendre les subtilités des substances que l’on envisage.
Dans le monde du culturisme et du sport, une substance qui
a suscité une consideration considérable est l’énanthate de testostérone.Lorsque l’on considère ses avantages en termes de positive aspects potentiels et de pressure par rapport à ses effets
secondaires potentiels et à son profil, il peut être considéré comme un stéroïde anabolisant très raisonnable à cet
égard. L’acide énantoïque est attaché au groupe hydroxyle 17-bêta sur le squelette de la
testostérone. Les stéroïdes anabolisants estérifiés sont plus liposolubles et se libèrent lentement du
website d’injection. Cependant, ce n’est pas la principale raison pour laquelle les
esters prolongent le taux de libération du stéroïde anabolisant.
Le trenbolone est un stéroïde anabolisant
de niveau avancé uniquement et ne doit pas être touché par les débutants.Étant un produit de la testostérone, les effets secondaires androgènes
sont également à prévoir. La peau grasse, acné, l’agressivité, le visage/corps de
la croissance des cheveux et la calvitie masculine, tout est possible.
Plus âgés ou les personnes sensibles peuvent donc choisir d’éviter les produits de la testostérone, et de regarder
vers plus doux anabolisants comme DecaDurabolin ou Equipoise qui produisent moins d’effets secondaires.
D’autres peuvent choisir d’ajouter la drogue
Proscar/Propecia, ce qui permettra de réduire au
minimal la conversion de la testostérone en DHT (dihydrotestostérone).
Avec des niveaux de sang de ce métabolite particulièrement réduite, l’incidence des effets indésirables liés à la doit
aussi être réduit. Avec une forte bulking drogues cependant, l’utilisateur va généralement s’attendre à subir des effets secondaires forts et souvent les tolérer.Les effets androgènes de la testostérone peuvent compléter les effets brûle-graisses d’Anavar, mais avec une certaine rétention d’eau temporaire.
Anavar (Oxandrolone) est un oral, considéré comme l’un des stéroïdes anabolisants les plus sûrs du marché (aux côtés de la testostérone).
La trenbolone, comme la testostérone, est un injectable ; il n’y a
donc pas d’effets néfastes sur le foie avec ce cycle.
Bien que Dianabol ne soit pas exceptionnellement androgène, l’acné et
une hypertrophie de la prostate sont des effets secondaires
possibles, en raison de la présence de testostérone.Si dans des cas individuels, des �rections fr�quentes
ou persistantes apparaissent, la dose doit �tre r�duite
ou le traitement interrompu afin d’�viter des l�sions du p�nis.TESTOSTERONE DESMA 250 mg/1 mL, resolution injectable en traitement de substitution peut r�duire la spermatog�n�se de mani�re r�versible (voir rubriques four.eight et
5.3). Une surveillance accrue du temps de prothrombine et la d�termination de l’INR
sont recommand�es. Adaptation de la posologie de l’antagoniste de la vitamine K pendant le
traitement androg�nique et � son arr�t. TESTOSTERONE DESMA 250 mg/1 mL, answer injectable doit
�tre arr�t� d�finitivement si des sympt�mes li�s � des concentrations s�riques d�androg�nes trop importantes persistent ou r�apparaissent en cours
de traitement avec le sch�ma d�administration recommand�.
Si, dans certains cas, des �rections fr�quentes ou persistantes apparaissent,
la dose doit �tre r�duite ou le traitement interrompu afin d’�viter toute l�sion du p�nis.
Aucune �tude n�a �t� r�alis�e pour d�montrer l�efficacit� et la tol�rance de TESTOSTERONE DESMA
250 mg/1 mL, resolution injectable chez les sufferers souffrant d�insuffisance r�nale ou h�patique.Dans cet article, nous explorerons les détails
d’un cycle optimum d’énanthate de testostérone, démystifiant
les dosages, la fréquence et les considérations tant pour les débutants que pour les athlètes expérimentés.
Il ne sera pas difficile d’acheter de l’énanthate en Ukraine si vous êtes shopper de
notre magasin de stéroïdes Hulk Shop. Ici, vous avez
la possibilité d’en savoir plus sur les caractéristiques, la politique de prix des médicaments stéroïdiens et d’acheter de la testostérone qui
contient d’autres chaînes essentielles. Après avoir passé une commande,
vous recevrez une livraison rapide dans n’importe quelle
ville du pays sans quitter votre domicile. Nous apprécions nos purchasers et nous soucions
de notre propre réputation, c’est pourquoi nous ne vendons que des produits de haute qualité
de fabricants renommés.
De nombreux sportifs utilisent ce médicament dans le traitement
de l’usure des disques intervertébraux. Il convient de noter qu’avec l’aide
de ce médicament, les processus de régénération sont également
accélérés, les processus de motivation et le tonus général du corps sont augmentés.Beaucoup d’hommes baissent un peu leur total de milligrammes par semaine à mesure que le spectacle se rapproche;
cela dépend du sort et de la qualité de sa réaction et de la quantité d’eau qu’il retient
en raison de la présence d’hormones. Pour le culturiste prêt à la compétition, il s’agira généralement d’un cycle de testostérone
qui lui est réservé et il constatera que le dosage est généralement
le même que celui de son cycle de testostérone hors saison, à
quelques exceptions près. Beaucoup d’hommes se contentent d’un dosage thérapeutique pendant quelques semaines avant d’entamer une nouvelle phase de poussée ou, comme c’est souvent le cas, d’entrer dans leur cycle de compétition. Un cycle avancé de testostérone pour le bulking est généralement réservé aux personnes extrêmement difficiles;
nous parlons ici d’hommes qui vivent et respirent la efficiency dans tous les features de leur vie.Un tel cycle de testostérone peut être utile et très efficace dans
presque tous les cas, en réduisant ou en augmentant le quantity et, dans de nombreux cas, ce sera toute la testostérone dont certains
auront besoin.
Anadrol provoquera une augmentation rapide des enzymes AST et ALT; tous
deux étant des marqueurs de stress hépatique.
C’est l’une des piles de stéroïdes, sinon la plus sûre, que les bodybuilders peuvent prendre.
Un PCT agressif de hCG, Nolvadex et Clomid sera également nécessaire sur ce cycle Test/Tren pour éviter un crash presque certain (et pour aider à solidifier les
gains). L’élément unique de cette pile
est qu’elle est très androgène, donc il y aura une perte de graisse considérable ; ainsi que
des gains de force/muscle exceptionnels. La testostérone et le Deca Durabolin font exception à cette règle,
les deux composés n’affectant pas le foie et n’ayant que des impacts modestes sur le cholestérol dans
nos LPT (tests de profil lipidique). -
High Testosterone Joint Pain
After this peak, testosterone ranges gradually decline all
through the day, with the lowest ranges usually occurring in the late afternoon or early evening.
One frequent physiological reason is polycystic ovary syndrome (PCOS), a hormonal dysfunction characterized by enlarged ovaries with small
cysts and elevated androgen ranges. PCOS disrupts the normal
balance of hormones in the body, leading to symptoms corresponding to hirsutism (excessive hair growth), zits, and irregular menstrual cycles.
Excessive testosterone ranges in women, known as hyperandrogenism, may result from
various underlying causes, each physiological and pathological.Different factors contributing to low testosterone in girls include
medical circumstances such as hypothalamic
or pituitary issues, and primary ovarian insufficiency (premature ovarian failure).
Additionally, sure medications similar to oral contraceptives,
glucocorticoids, and opioids may suppress testosterone production.
However the best solution is working with a healthcare professional
you belief to receive correct analysis and recommendation on available remedy choices.One of the widespread concerns about saliva testosterone checks is their accuracy compared to blood exams.
However, analysis has shown that saliva testing is a dependable methodology
for measuring free testosterone ranges, supplied that proper assortment and handling procedures are adopted.
It is necessary to decide on a high-quality testosterone e check package from a reputable supplier to ensure
correct results. At-home testosterone testing kits, including
saliva-based ones, are designed to be user-friendly and convenient.
A testosterone e take a look at kit sometimes consists of detailed instructions,
a saliva collection tube, and a pay as you go envelope for returning the pattern to a
certified laboratory.
As such, figuring out testosterone levels is a vital a half of diagnosing and treating circumstances
such as hypogonadism and infertility, amongst others. When it comes to checking testosterone levels, most individuals are conversant in the
usual blood test. This involves taking a blood sample and measuring the quantity of testosterone present in the blood.Nonetheless, there are actually several other exams that can be utilized to examine testosterone levels, every with its own benefits and downsides.
They can also provide extra information about a person’s
overall hormone steadiness and help guide remedy decisions.Monitoring testosterone levels is important for men who want
to maintain optimal health, performance,
and vitality. Nonetheless, frequent visits to
a healthcare supplier for testing is probably not handy for everybody.
This is where at-home testosterone checks, particularly saliva testosterone checks, come into play.People ought to at all times talk about their at-home
take a look at outcomes with a physician earlier than making any well
being decisions. Testosterone levels are often highest in the morning and
lowest within the evening. At-home tests or healthcare professionals will probably recommend testing in the morning to realize essentially the most
accurate end result. The take a look at requires them
to collect a blood sample using the finger prick method and return it to considered
one of its CLIA-certified laboratories. Quest states an individual should fast in a single day for 10 to 12 hours earlier than taking this
take a look at. It additionally advises people to arrange an appointment
within the morning, when it’s best to measure testosterone levels.Though Labcorp is typically known for its in-person checks, it
uses a third-party firm known as Getlabs to assist folks take at-home exams.Saliva exams have turn out to be increasingly in style for measuring testosterone levels
as a outcome of their convenience and non-invasive
nature. Nonetheless, there are some important limitations and considerations that should be taken under consideration when utilizing saliva tests for testosterone measurement.
In addition to considerations about accuracy, the reliability of saliva tests can be some extent of discussion. Saliva
tests could be influenced by numerous elements, corresponding to diet,
medicine, and oral health. For instance, sure drugs, corresponding to oral contraceptives and corticosteroids, can intrude with the accuracy of saliva exams.
Moreover, oral health points, such as gum
illness and bleeding gums, can contaminate saliva samples and affect the outcomes.
Due To This Fact, it’s crucial to contemplate these elements when decoding saliva
check outcomes to ensure their reliability.
On the opposite hand, high testosterone levels can even have unfavorable
effects, including aggression and pimples. Saliva samples provide a non-invasive methodology for measuring salivary
testosterone levels, permitting for comfort and ease of collection in comparability with conventional blood exams.
EmpowerDX presents an at-home hormone test to measure estradiol (a type of the hormone estrogen), dehydroepiandrosterone sulfate (DHEA-S) and total testosterone levels.
The price of the check kit includes shipping and a physician-reviewed take
a look at end result. Samples are assessed in CLIA-certified labs and results are delivered within two
days of pattern receipt and are available in an easy-to-read format.The Nationwide Library of Medicine mentions that you may
want hormone alternative therapy, or more particularly,
testosterone alternative remedy (TRT) [4, 5].
The symptoms of low testosterone are lowered libido,
decrease muscle mass, lowered power, increased physique fats, low temper, and fatigue
[2]. That said, saliva testing will inform you the amount of testosterone that has diffused into your
saliva but can’t provide you with info on testosterone that is bound
or used in your body. Keep studying to find out about these exams
and the means to enhance your testosterone levels.She was beforehand the health and commerce editor at Men’s Well Being, the place she examined
and reported on the most recent, buzziest health
and wellness products to hit the market. As a NASM-certified private coach
and Precision Nutrition-certified diet coach, she is enthusiastic about supporting girls at the
intersections of health, food, and community. Earlier Than coming
into journalism full-time, Talene was a personal chef for
4 years and nonetheless enjoys cooking for and internet hosting friends and family frequently.
For standardization, asprosin hormone was diluted with 1 ml standard and
TNF-α was diluted with 0.5 ml standard and gently shaken for 10 min with out foaming.
The prepared asprosin commonplace focus was 40 ng/mL and TNF-α was
1,000 pg/mL. Serial dilutions were created from the standard concentrations prepared as inventory options. -
Blanche
For more information about the connection between Hone and
the medical practices, click on here. Hone’s at-home testosterone evaluation is the best approach to uncover whether or not
your levels are low. Mayo Clinic notes that these circumstances can include sure inflammatory diseases that impression the pituitary gland and hypothalamus—which each affect testosterone production. TRT injections bypass hepatic metabolism, not like oral formulations,
guaranteeing excessive bioavailability. Nonetheless, a significant disadvantage is the hormonal fluctuation between doses.Moreover, following the prescribed hormone remedy routine
and attending all follow-up appointments can ensure the greatest possible outcomes.
Discussing any issues or questions with a healthcare provider can provide
additional steerage on optimizing the effects of testosterone pellets.
In addition to the duration of the consequences, it is necessary to consider the potential
unwanted effects of testosterone pellet remedy. Some people might experience short-term irritation or bruising on the web site of the
pellet insertion. There is also a danger of infection or pellet extrusion,
although these problems are uncommon when the process is performed by a skilled healthcare supplier.They might help you identify if testosterone pellets are the best alternative for you
and reply any questions you may have about the treatment.
First, the regular launch of testosterone helps
to take care of steady hormone levels, which can lead to improved temper, power levels, and sexual perform.
Additionally, as a outcome of the pellets are implanted underneath the skin, there
is not any need for day by day injections or lotions.
Testosterone pellets are a type of testosterone alternative therapy (TRT) that provide a quantity of advantages over other
types of TRT.
This may end up in a rollercoaster-like sequence of modifications in mood, sexual exercise, and vitality levels.It is price noting that the period of the effects can differ based on the dosage
of testosterone pellets which are used. Larger dosages might present longer-lasting results, whereas decrease
dosages might require extra frequent reinsertion of the pellets.
If you’ve found reduction from hormone-related issues with hormone pellet therapy, you know the
feeling of renewed energy, balanced mood, and general well-being.
Another downside is that due to the sluggish launch of T from testosterone pellets, it’s
a lot more durable to dose them accurately for brand spanking new patients.It can increase libido, improve muscle mass, sharpen memory, and bump up vitality.
In 2025, clinics like AlphaMan, a men’s well being
heart specializing in hormone optimization, are rethinking how
testosterone therapy fits into trendy masculinity. As A End Result Of when it comes to low testosterone, the
stakes lengthen far beyond the health club. Even high-performing males balancing careers, households, and health can find themselves battling unexplained fatigue, diminished focus, low libido, and
chronic sluggishness regardless of sufficient relaxation. Due To
This Fact, traces of testosterone from the pellets
can remain in your system for as long as a yr.
As A End Result Of everybody responds to hormone alternative remedy in another
way, you might feel a difference after a few days out of
your first appointment, or after a couple of appointments.
Bioidentical estrogen replacement remedy is considered elective and is not
lined by insurance. You might feel a distinction after a couple of
days from your first appointment, or after a couple of appointments.
Patients have reported enhancements within a couple of
weeks, however full outcomes may take up to six weeks. The time it takes is dependent upon how
your body responds to the remedy and the severity of your hormone imbalance.When it involves this type of hormone deficiency treatment, the time it takes for them to
take effect varies from individual to individual.Each affected person is exclusive, and their physique chemistry plays a significant function in how the pellets are absorbed and
utilized. Usually, reduction of deficiency signs can happen anywhere from a
number of days to three weeks. Nonetheless, it’s essential to
note that short-term and long-term results of testosterone pellets differ.
To diagnose testosterone deficiency, medical doctors might perform blood tests to measure testosterone
ranges in the physique.
At the identical time, higher levels of bodily activity
can promote faster blood circulation and pellet breakdown.
Additionally, the position of the pellet insertion performs a
job, as these positioned nearer to blood vessels may dissolve more quickly.Moreover, your general health and hormone levels can also affect the
rate of pellet dissolution. Discussing these elements with
your healthcare provider to make sure optimum
hormone pellet dissolution is crucial. The expected
vary for testosterone pellet dissolution can range based mostly on particular person factors. -
https://ezonnerecruit.com/employer/viagra-testosterone
A total of 40 individuals had been put in each of case and control teams.
This is when a breast most cancers tumor of any size has spread to the
breast skin or chest wall and to nine or fewer lymph nodes in the area.At Present, a bunch of various genomic markers may help determine customized treatment options.
However at the time of Randee’s initial analysis,
there have been limited therapy choices obtainable tailor-made to particular genomic markers.It is utilizing hormones which would possibly be similar to the hormones naturally
made by your physique. Bioidentical hormone replacement therapy (BHRT) offers an alternative
to artificial hormones, like some types of injectable testosterone or Premarin. If you’re thinking about a more natural method to hormone remedy, bioidentical
hormone replacement may be suitable for you. Some hormones circulating within the bloodstream, such because the thyroid hormones and
insulin, don’t enter the saliva because of their giant size; which
means saliva hormone checks cannot measure these hormones. A hormonal imbalance happens when your hormones
are too high or too low. The imbalance signifies a deficiency in a particular hormone, whereas some may present an overflow.
The Estradiol test measures the amount of the hormone estradiol within the blood.The greatest way to check for adrenal fatigue or adrenal
dysfunction is with urine and saliva testing. We are capable of assess steroid metabolites for DHEA, metabolized/free cortisol,
and the cortisol awakening response (CAR),
which are players in evaluating adrenal fatigue. Totally
Different docs and healthcare professionals may have their own opinions
and preferences with how and what they check and typically are based mostly on a patient’s particular set of signs.This submit will map out the several types of hormone
tests, their benefits and downsides, and guide you on how to take a look at for particular hormones.
Hormonal imbalance checks are being used greater than ever before, and
new analysis demonstrates a hyperlink between hormones and bodily abnormalities seen in girls on a
daily basis. When the body produces too much or too little of any one of the many hormones that
handle our organs and methods, it can cause an imbalance.Fertility is also depending on wholesome hormone signaling and communication. High stress, anovulation (as usually
happens in PCOS), fibroids (which often happen in a high-estrogen environment),
and different hormone-related components can all negatively
influence fertility. Luckily, early identification boosts your chances of beating most cancers.
That Is why you must report signs of hormone imbalance to your provider immediately.If your estrogen ranges drop due to an imbalance, it might possibly cut back vaginal fluids and cause tightness.
That’s why it’s frequent for headaches to strike right before or throughout your period,
when estrogen is on the decline. Regular headaches or ones that always
floor across the identical time every month can be a clue that your ranges of this hormone
could be shifting. This can happen during menopause, when your pores and skin naturally begins to
thin and can’t maintain onto as much moisture because it used to.To restore stability and hormonal concord, name Women for Women OBGYN, SC, or simply click the web scheduler today.
There is not any single check that medical doctors use to diagnose hormone imbalance.
Nonetheless, they begin by bodily analyzing you and asking crucial questions to understand your situation.
Vaginal dryness can change estrogen levels, and applying lotions containing estrogen might help scale back symptoms.
The Insulin-Like Development Factor 1 (IGF-1) test measures levels
of IGF-1, a protein that is intently associated to growth components.
Our IGF-1 blood check is commonly used to measure levels of human growth hormone (hGH) and its exercise.Measuring these hormones is commonly useful in screening for reproductive disorders, menstrual
irregularities, and fertility issues. This contains widespread conditions and hormonal
patterns like premenstrual syndrome (PMS), estrogen dominance,
polycystic ovary syndrome (PCOS), menopause, and heavy menstrual cycles.
Nonetheless, DUTCH testing can present a picture of hormonal fluctuations throughout a full menstrual cycle, which can be helpful for people with chronic hormonal imbalances or who suspect infertility.
Symptoms like temper swings, low intercourse drive
and sizzling flashes could also be a sign of hormone imbalance.Hormonal imbalances have gotten part of on a regular
basis life for many ladies, typically to the point of disrupting their well-being and creating many
troublesome signs. Sleep issues, joint pain, reminiscence loss,
fatigue, and temper disturbances are all signs that there may be one thing off along with your hormone ranges.There are less-common hormonal imbalances, too, like Cushing’s syndrome and Addison’s disease.
Solely a health care provider can help identify which hormonal imbalance you’re experiencing
and what course of treatment is best. Aside from medical treatment,
your supplier might advocate sure lifestyle changes to help handle a hormonal
imbalance, similar to managing your stress levels and getting routine exercise.
Many dietary dietary supplements in shops claim to treat different hormonal imbalances,
but few of them have been scientifically proven to have a useful effect.
It’s necessary to all the time talk to your healthcare supplier first about taking dietary supplements.The HPA axis is your central stress response system, where your endocrine system and central nervous system work together.
Then it turned out my pal had also received pushback on hormones form the same physician. Welcome to AskWomenOver30, an inclusive Reddit neighborhood where folks can ask
query to and focus on subjects with women over the age of 30.All are welcome, please learn and abide by the foundations in our
sidebar.
One is the Women’s Hormone Test, for girls and other people AFAB,
which evaluates 10 of the important thing feminine reproductive hormones,
similar to progesterone, estrogen, and cortisol amongst others.
If you suspect that you’re experiencing a hormonal imbalance or the
negative effects of age-related hormone fluctuation, it’s a good idea to start recording your signs
every day. This record can be an essential software whenever you converse to a hormone specialist and begin the journey of analysis and therapy. -
https://hireforjob.com/Employer/how-long-is-testosterone-detectable-In-blood
It will take between 4 and 6 weeks to extend testosterone production utilizing natural testosterone boosters, relying on a person’s response to
the complement. Nonetheless, adjustments in lean muscle growth and
vitality might take as a lot as 6 months.
D-aspartic acid is the most important ingredient in almost every pure
testosterone booster. It helps make customers more muscular
and shredded, all due to optimal testosterone levels.
WOWMD Testosterone Help works by helping to increase testosterone
and energy levels. Common use may assist higher performance in physical actions,
contributing to muscle achieve and prostate well being.Testolab Pro® is handiest when taken as part of a strength
and cardio fitness regimen. You also won’t have to cycle this supplement, as it’s designed for long-term use
and reportedly “gets stronger the longer you take it.” It’s necessary to observe dosage instructions and consult with a healthcare skilled
if you expertise any uncommon signs. It’s necessary to note that particular person outcomes could
differ, and Provacyl is not intended to diagnose,
treat, remedy, or forestall any illness. However, with a 67-day money-back assure,
customers can really feel assured in attempting Provacyl and experiencing its potential advantages for themselves.
This is the only product out there that is formulated with all 12 of those components
in these actual doses.
Tribulus Terrestris, regardless of its popularity as a testosterone booster, has not been conclusively confirmed to have a significant influence on testosterone ranges in people.TestoFuel additionally makes use of D-Aspartic Acid, which has been shown to spice up testosterone in males with low T by as
a lot as 60% [4]. TestoFuel additionally consists of excessive concentrations of zinc,
magnesium, fenugreek, ginseng, boron, and maca root.Helping to assist wholesome testosterone, improve your temper, cut
back cortisol, and enhance your vitality ranges.
Out of the dozens of testosterone dietary supplements we tested, TestoPrime takes the primary spot for the all-around best model.
Thus, it’s important to have sufficient sleep, eat a healthy
and well-balanced food regimen, keep active, meditate, and chill out to scale
back stress and naturally enhance low testosterone
ranges. But, all of them have the effect of boosting the production of testosterone
ranges in the gonads and adrenal gland, which in turn bolsters your capability to push through bodily limitations that used to restrict your
efficiency within the health club.
The major ingredient, D-Aspartic Acid, plays a pivotal position in boosting testosterone.
Studies show that this amino acid has a significant impression on rising testosterone
levels by stimulating the production of luteinizing hormone (LH), which in flip enhances testosterone synthesis.
Take A Look At Drive Testosterone Booster Supplement for Men & Ladies,
consists of highly effective boosters formulated to help
free testosterone levels, fight feelings of lethargy and lack of muscle mass,
and give you the stamina. AlphaTest is a mainly herbal blend that focuses on a few of the most-proven testosterone boosters.
The complement includes zinc, a solid 300 mg
of fenugreek extract, and tribulus terrestris, but less in the best way
of nutritional vitamins and non-zinc minerals.
It functions by stimulating the discharge of luteinizing hormone, which
aids in testosterone production, and by growing
the rate of free testosterone from the binding hormone sex-hormone-binding-globulin (SHBG).
Moreover, Tongkat Ali might enhance libido, erectile perform, muscle mass, physique composition, and mood.
As men age, their pure testosterone ranges begin to decline, which might result in a lack of muscle mass and strength.Testosterone boosters might help to increase
testosterone ranges in males over 50, which might enhance muscle growth and energy.We have personally used Nutrex Research Anabol Hardcore,
Anabol PM, and Alpha-T Muscle Building Bundle and have seen spectacular outcomes by method of muscle development, energy, and endurance.
Anabol is a strong adaptogenic supplement that helps sign the physique to
extend muscle protein synthesis, which might lead to sooner muscle-building and recovery.
Anabol PM is a good nighttime muscle builder that helps enhance muscle restoration and increase lean muscle growth.However, there are some crucial variations in the ingredient lists that lead us
to favor TestoPrime over Testogen. Ultimately, TestoPrime includes more of the
better-researched testosterone-boosting elements. You might theoretically make up for the difference
— and even get a greater general impact — by taking both
Testogen’s capsules and its drops, however that combination will get costly.
Most of the research into ginseng’s potential as
a testosterone booster has taken place in rats and mice.13 The results are compelling, but extra human trials are needed.
For now, there are more essential elements to look for in a testosterone booster.Despite that little little bit of subterfuge, a lot of the
other ingredients seem right here at sufficient doses to tackle
totally different aspects of aging. We’ve gone over most already,
but we should always level out that sodium hyaluronate is a type of hyaluronic acid,
and its dose here aligns properly with research into skin well being.
The theory goes that a large dose can knock out senescent cells more successfully, nevertheless
it doesn’t make sense to take that bigger dose every day,
as new senescent cells haven’t fashioned yet. -
https://femdel.com/employer/ovaires-polykistiques-testosterone/
Ce médicament s’utilise pour remplacer la testostérone des hommes atteints d’affections
causées par une déficience en testostérone. Cypionate de testostérone jouera
également un rôle essential autour de la créatine. La créatine est essentielle à l’adénosine triphosphate (ATP), la
source d’énergie de nos muscular tissues et lorsque les muscular tissues
sont stimulés, l’ATP est décomposé en adénosine diphosphate (ADP) et c’est ce qui libère de
l’énergie. Malheureusement, le processus est souvent trop lent lors d’une activité
intense, mais grâce à l’utilisation de la testostérone Cypionate, cette demande est satisfaite
car l’ATP est reconstitué à un rythme beaucoup plus rapide.En d’autres mots, la Testostérone Cypionate augmente aussi l’efficacité de la répartition des éléments nutritifs,
vous stockez plus de muscles et moins de graisse !
La Testostérone Cypionate jouera également un rôle essential au niveau de
la créatine. La créatine est essentielle à l’Adénosine
Triphosphate(ATP), la source d’énergie pour nos muscles, et lorsque les muscular tissues sont stimulés l’ATP se décompose en Adénosine Diphosphate(ADP) et c’est ce qui crée l’énergie
musculaire.
L’interférence d’un médicament avec un autre n’entraîne
pas toujours l’interruption de la prise de l’un d’eux. Demandez à votre médecin quelle est la conduite à tenir en cas d’interactions médicamenteuses.
Ne donnez pas ce médicament à quiconque, même à quelqu’un qui souffre des mêmes
symptômes que les vôtres.
Le cypionate de testostérone est utilisé pour traiter les symptômes d’hypogonadisme
chez les hommes. Dans cet état, les hommes ne produisent pas
assez de testostérone, l’hormone sexuelle.
Le cypionate de testostérone ne devrait s’utiliser que
si la déficience en testostérone a été confirmée
par les symptômes et les analyses de sang. La testostérone
est facilement l’hormone la plus efficace qui peut être utilisée pour la
musculation. Il augmente la masse musculaire, et joue également
un rôle majeur dans nos décisions et sans libido. La testostérone
peut être définie comme la conquête, le désir, la sexualité, le dynamisme
et la drive.
Si vous êtes nouveau avec l’utilisation des stéroïdes anabolisants et que
vous avez déjà optimisé votre potentiel naturel, c’est le stéroïde idéal pour voir vos
progrès continuer au-delà de la normale.
Si vous êtes un utilisateur de stéroïdes de longue date
et que vous avez déjà utilisé Cypionate lors de cycles précédents, ce Testostérone continuera à être toute aussi
efficace à chaque fois. Une autre motion indirecte de la Testostérone pour la perte
de graisse est l’effet de fragmentation des éléments nutritifs des
muscular tissues et des graisses. Le corps fabrique continuellement du muscle, et ce rythme s’accélère si vous augmentez les quantités de nourriture qui vont directement rejoindre les tissus musculaires
au lieu d’être stocké sous forme de graisse.La answer injectable de cypionate de testostérone est utilisée pour le
traitement à long terme. Cela comporte de graves risques si vous ne prenez pas le médicament tel qu’il vous a
été prescrit.
Une autre motion indirecte de la perte de graisse produite par la testostérone est l’effet
de portionnement des nutriments qu’elle a sur les muscle tissue et la graisse.Étant donné que le corps construit des muscle tissue à un rythme accéléré, une plus grande partie de la nourriture que vous mangez est acheminée vers les tissus musculaires au lieu d’être stockée sous forme de
graisse, l’efficacité des nutriments est améliorée.
Au cours de cette période d’utilisation,
nous sommes alors en mesure de préserver le tissu musculaire maigre beaucoup plus
facilement qui serait autrement perdu. En vue de perdre du gras corporel, il faut brûler plus de calories que nous en consommons
et cela peut souvent conduire à la perte de volume des muscles et la perte de drive.Quel que soit le dosage total ou la longueur des cycles, vous aurez besoin de mettre
en place une thérapie post-cycle (PCT) une fois que votre treatment de
testostérone Cypionate sera terminée. Pour la plupart des hommes, si vous êtes en cours d’arrêt de l’utilisation de stéroïdes anabolisants pendant plus de dix semaines,
vous aurez besoin d’une PCT, mais si votre période est inférieure, alors elle peut être ignorée.
Il est à noter, quand il s’agit de dopage des performances, la testostérone Cypionate n’est pas recommandée pour les femmes.
Cypionate de testostérone est une model synthétique de l’hormone de testostérone produite naturellement.Cette hormone est responsable de nombreuses caractéristiques physiques et mentales différentes chez les hommes.
Les IA sont les plus efficaces, mais ils peuvent aussi se révéler problématiques au niveau du cholestérol, la prudence est
conseillée, et nous vous recommandons simplement le Novaldex.
Au-delà de ces effets, la Testostérone Cypionate peut favoriser la dihydrotestostérone
(DHT) responsable d’effets secondaires tels que l’acné, la
perte de cheveux et l’élargissement de la prostate.
En vue de fournir une safety à ce niveau-là, un inhibiteur de la 5-alpha-réductase comme le Finasteride peut être utile automotive c’est un suppresseur
d’androgènes. Il faut noter que la perte de cheveux n’est possible que chez les hommes de toute façon prédisposés à la calvitie masculine.Testosterona C est un stéroïde injectable qui contient 200 mg par ML de l’hormone testostérone Cypionate.
L’ester Cypionate de ce médicament ralentit sa libération et nécessite donc que les injections soient moins fréquentes qu’elles ne le seraient si un bodybuilder utilisant du propionate
de testostérone. Les athlètes utilisant ce stéroïde trouvent souvent qu’un programme d’injection deux fois par semaine, comme le lundi/jeudi, est très suffisant pour
maintenir des taux sanguins stables de l’hormone.
La testostérone est l’hormone anabolisante la plus courante et est également considérée comme la plus fondamentale.
Pour cette raison, les bodybuilders le considèrent souvent comme le stéroïde de base de la plupart
des cycles. Les utilisateurs de ce stéroïde remarqueront un acquire spectaculaire de taille
et de force musculaire, ainsi qu’un sentiment général de bien-être et une augmentation de la libido
et de la libido.
La dose habituelle de cypionate de testostérone pour les
hommes adultes est de 200 mg toutes les deux semaines, jusqu’à un most
de 400 mg par mois. Un médecin pratique l’injection dans le muscle grand
fessier (dans la région des fesses). La dose typique de cypionate de testostérone chez un culturiste
se situe entre 500 et 1250 mg par semaine et pour une durée de cycle de eight
à 20 semaines, en fonction bien sûr des objectifs de l’athlète.Le Cypionate favorise la rétention d’azote dans le muscle,
et plus d’azote les muscles détiennent, plus de protéines les
muscular tissues stockent. -
Quel est le taux normal De testostérone chez l homme
Le cypionate de testostérone est utilisé pour traiter les symptômes d’hypogonadisme chez les hommes.
Dans cet état, les hommes ne produisent pas assez de
testostérone, l’hormone sexuelle. Le cypionate de testostérone ne devrait s’utiliser que si la déficience
en testostérone a été confirmée par les symptômes et les analyses de sang.
La testostérone est facilement l’hormone la plus efficace qui peut être utilisée pour la musculation. Il
augmente la masse musculaire, et joue également un rôle majeur dans nos décisions et sans libido.
La testostérone peut être définie comme la conquête, le désir, la sexualité, le dynamisme et la
force.
Assurez-vous d’informer votre médecin de tous les
médicaments, vitamines ou herbes que vous prenez.
Pour savoir remark ce médicament pourrait interagir avec quelque selected d’autre que vous prenez, parlez-en à votre médecin ou
à votre pharmacien. Ne jetez pas de médicaments dans les eaux usées
(par ex. pas dans l’évier ni dans la cuvette des cabinets) ni avec les ordures ménagères.
Demandez à votre pharmacien remark vous débarrasser des médicaments
inutilisés ou périmés. Ce médicament est disponible sous
divers noms de marque ou sous différentes
présentations, ou les deux. Une marque spécifique de ce médicament n’est peut-être pas offerte sous toutes
les formes ni avoir été approuvée contre toutes les
affections dont il est query ici.
La dose habituelle de cypionate de testostérone pour les hommes
adultes est de 200 mg toutes les deux semaines, jusqu’à un maximum de four hundred mg par mois.Un médecin pratique l’injection dans le muscle grand fessier (dans la
région des fesses). La dose typique de cypionate de testostérone chez
un culturiste se situe entre 500 et 1250 mg par semaine et pour une durée de cycle de eight à 20 semaines, en fonction bien sûr des objectifs de l’athlète.Le Cypionate favorise la rétention d’azote dans le
muscle, et plus d’azote les muscles détiennent, plus de protéines les muscles stockent.De plus, la testostérone Cypionate a la capacité d’augmenter la
manufacturing de globules rouges et un nombre plus élevé
de globules rouges améliorera l’endurance grâce à une oxygénation accrue
dans le sang. Plus de globules rouges peuvent également
améliorer la récupération après une activité physique intense.Même ainsi, les effets anabolisants / androgènes de la testostérone dépendent de la dose, plus la dose est élevée, plus l’effet de renforcement musculaire est élevé.
La testostérone se lie relativement bien aux récepteurs androgéniques, ce qui provoque la dégradation des
graisses et empêche la formation de nouvelles cellules
graisseuses. La testostérone cypionate est un ester injectable à libération lente de l’hormone mâle anabolisante, la testostérone.
Cette model du cypionate de testostérone est l’un des produits de prise de
masse les plus efficaces qui existent. Il a des effets spectaculaires sur la taille des muscle
tissue et sur l’augmentation de la force et a une demi-vie
d’environ 8 jours, ce qui permet d’avoir à l’injecter moins
fréquemment. Avec un cycle de testostérone cypionate bien planifié,
presque tous les avantages des stéroïdes anabolisants peuvent être obtenus.Dans le cadre d’une sèche ou de prise de masse maigre, la masse musculaire maigre peut être facilement construite et la graisse corporelle
fortement diminuée. Pour ce qui est de la prise de masse, vous devrez consommer
suffisamment de energy, mais une légère accumulation de graisse se produira.La testostérone Cypionate est une hormone hautement anabolisante
et androgène, ce qui en fait un wonderful stéroïde à utiliser si l’on recherche plus de taille et de
drive. Cypionate de testostérone favorise la rétention d’azote
dans le muscle et plus les muscular tissues contiennent d’azote,
plus les muscles stockent de protéines. Cypionate
de testostérone peut également augmenter les niveaux d’une autre hormone anabolique, IGF-1 dans le tissu musculaire, fournissant encore plus
d’activité anabolique. Cypionate de testostérone a également la capacité étonnante d’augmenter l’activité
des cellules satellites. La testostérone se lie également au récepteur des androgènes pour favoriser les mécanismes dépendants des récepteurs des androgènes pour le achieve musculaire et la perte de graisse.Si les effets secondaires vous inquiètent, discutez des risques et des bienfaits de ce médicament avec
votre médecin. Lancez une recherche en tapant « testostérone, cypionate de » pour trouver des marques qui sont encore offertes.
Si vous utilisez ce médicament, discutez avec votre médecin ou un pharmacien de vos options thérapeutiques.
Comme les taux d’œstrogènes augmentent, cela peut conduire à la gynécomastie (élargissement du sein masculin) et la rétention d’eau en excès.
Gardez ces considérations à l’esprit si votre médecin vous prescrit du cypionate de
testostérone. Pour aider à éviter les interactions, votre
médecin devrait gérer tous vos médicaments avec soin.
En raison de sa capacité à augmenter la taille et la pressure musculaire, c’est sans doute la forme de testostérone la plus populaire utilisée
aujourd’hui. C’est une hormone très bien tolérée par la plupart des hommes, et les effets secondaires de la Testostérone Cypionate
sont à bien des égards très faciles à contrôler.
Quand il s’agit de parler des effets indésirables de la Cypionate, gardez à
l’esprit qu’ils sont simplement possibles et ne sont nullement garantis.
La dose totale de testostérone, les prédispositions génétiques et votre état
de santé général joueront un rôle dans l’apparition de ces effets ou
non. En ce qui concerne les effets secondaires eux-mêmes,
comme tous les composés de testostérone,
Cypionate entraîne un haut niveau d’activité de l’enzyme
aromatase. La testostérone se lie également aux récepteurs androgènes pour promouvoir des
mécanismes spécifiques à ces récepteurs pour le gain de muscle et
la perte de graisse. La Testostérone Cypionate provoque des changements dans la forme,
la taille, et peut aussi changer l’apparence et le
nombre de fibres musculaires dans votre corps.
Bien que son utilisation pour la prise de masse soit la plus fréquente, les effets de la testostérone
cypionate peuvent être extrêmement bénéfiques lors d’une section de sèche.
Si vous êtes âgé de plus de sixty five ans, vous pourriez courir
un risque plus élevé de maladie cardiaque, de most cancers
de la prostate et d’hypertrophie de la prostate pendant que vous prenez ce médicament.
Ce médicament peut réduire la fonction hépatique et provoquer
une insuffisance hépatique. Un effet secondaire est une réponse indésirable à un médicament lorsqu’il est
pris à des doses normales. Il est essential que ce médicament soit employé conformément
aux indications de votre médecin. Si vous manquez un rendez-vous fixé
pour recevoir votre injection de cypionate de testostérone,
communiquez avec votre médecin aussitôt que
possible pour prendre un autre rendez-vous. La testostérone appartient à
la classe des médicaments appelés androgènes (des
hormones masculines). -
jobs.linttec.com
For molecules that are placed finish to end, the electrostatic interplay energy
becomes important. Turns out, this list is completely incorrect, and was apparently based
mostly on some flawed calculation of carbon atoms by Invoice
Roberts many years in the past. Not solely is it wrong, it is actually mistaken - in some cases,
half-lives are off by over 150%. It is recognised that there is variance of the peak and trough ranges between individuals(6) and
so the data can’t apply to everyone. We all have
a singular genetic blue-print, nobody person’s physiology
is identical to that of another. When selecting between Testosterone Undecanoate vs Decanoate, medical service professionals must
keep in mind age, comorbidities, life-style habits, and affected person favorities.Asymmetric unit of TUnd presenting non-hydrogen atoms at 50% probability level (a); general packing seen along the b-axis (b).
Asymmetric unit of TDec presenting non-hydrogen atoms at 50% likelihood stage
(a); total packing considered alongside a-axis (b). Asymmetric unit of TCyp presenting non-hydrogen atoms at 50% chance stage (a); overall packing viewed alongside c-axis (b).Uneven unit of Tena presenting non-hydrogen atoms at 50% probability
degree (a); overall packing viewed alongside b-axis (b). Contemplating the very large number
of scientific papers about this hormone, we thought of that it would be helpful to supplement it with studies associated to the construction, intermolecular interactions and solubility.Esters are essentially a category of organic compounds
that react with water to produce alcohols and organic or
inorganic acids. The testosterone molecule can solely turn out to
be bioavailable when enzymes from the liver break down the carbon chains releasing the testosterone.
The main position of hormones is to assist
keep homeostasis, a fancy course of that entails biochemical and physiological mechanisms to assist achieve an equilibrium or stability throughout the body.
By that rationale, the purpose of TRT and TOT is
to revive your levels and achieve stability.
Caproate is the slowest releasing ester used in Omnadren, which is why most athletes notice more
water retention with this compound as a end result of blood degree saturation. Whereas the
arrival of esters certainly constitutes a useful advance within the field
of anabolic steroid drugs, clearly you can see that there is not a magic concerned right here.
Esters work in a well-understood and predictable
method, and do not alter the exercise of the mother or father steroid in any
way aside from to delay its launch. Testosterone is testosterone
and anybody who’s going to let you know one ester form of this
(or any) hormone is significantly better than one other
one ought to perform a little more analysis, and so much less talking.
With a chain blocking the 17th beta place, binding to
the androgen receptor isn’t attainable (it can exert no activity in the body).
In order for the compound to turn into lively the ester should therefore first be removed.This is why we carefully titrate the prescribed dose of testosterone and HCG based on effect.
TRT must be personalised as we are all biologically distinctive, you can’t have a one dimension suits all
method to hormonal health. Additionally known as Hexanoic
acid; hexanoate; n-Caproic Acid; n-Hexoic acid; butylacetic acid; pentiformic acid; pentylformic acid;
n-hexylic acid; 1-pentanecarboxylic acid; hexoic acid;
1-hexanoic acid; Hexylic acid; Caproic acid.
This ester is similar to isocarpoate in terms of atom depend and weight, but is laid
out barely completely different (Isocaproate has a break up configuration, tough to elucidate right here however simple to see on paper).
Launch period would be similar to isocaproate (levels sustained for about one weak), perhaps coming barely nearer to enanthate because of its
straight chain.
Additionally known as Acetic Acid; Ethylic acid; Vinegar acid; vinegar; Methanecarboxylic acid.
Contrary to what you may have learn, acetate esters do not increase the tendency for fat removal.
This ester is used on oral primobolan tablets (metenolone
acetate), Finaplix (trenbolone acetate) implant pellets, and occasionally testosterone.
A fatty acid with ten carbon atoms is used to esterify testosterone into Testosterone Decanoate.
By delaying its release into the blood circulate, this
process extends the period of the medicine’s action. This subreddit is for questions and dialogue related to testosterone substitute therapy and testosterone.
It also focuses on lifestyle activities like exercise and diet for raising testosterone
levels naturally or the rest related to testosterone the substance.The four totally different testosterone esters on this
product actually look appealing to the patron, there is not a
denying that. But for the athlete I suppose it is all only a matter of selling (Hell, why purchase one ester when you will get four?).
If you have been present process testosterone
substitute remedy for example, you would in all probability
discover Sustanon a a lot more comfy option than testosterone enanthate .You would want to visit the doctor much less regularly for an injection, and blood
levels ought to be more steadily maintained between treatments.
But for the bodybuilder who is injecting 4 ampules of Sustanon per week, there is no advantage
over other testosterone merchandise. In truth,
the excessive price ticket for Sustanon often makes it a really poor purchase within the face of cheaper testosterone enanthate /cypionate .
Bodybuilders ought to probably stop looking on the four ester
problem, and stick with totals (Sustanon is just a 250mg testosterone ampule).Gold commonplace TRT includes Human Chorionic Gonadotropin (HCG) alongside testosterone.
I haven’t gone into detail on The Benefits of using HCG with TRT
or our TRT Management Pointers as these have been coated in earlier blogs.Anybody new to steroids could also be questioning what this means,
even some skilled steroid users may be questioning what this means.So right here in simple phrases you possibly
can read and hopefully understand all about steroid half life’s
and what this time period means. Analyzed Testosterone Decanoate vs Undecanoate can result in comparable unfavorable consequences of
HRT. -
Anabolic Steroids Reviews
The addition of a long appearing injectable base will present
your body with exogenous testosterone, which is one of the important hormones that drop when utilizing Dianabol.
A PCT plan normally follows after the utilization of Dianabol has ceased.
Usually, you’ll must take a combination of medication throughout this period to
revive normal HPTA features and remove estrogenic unwanted side
effects. For a primary time Dbol person, 20-30mg/day is throughout the
realm of secure. Your organs have an amazing capability to recover but should you abuse the drug, then you may be
setting yourself up for long-term harm.
Lately, steroids hit the highlight big time, fascinating each pros
and hobbyists aiming to stay king of the hill. Failure to implement an effective post-cycle therapy may also trigger long-term testosterone deficiency, negatively affecting
a person’s well-being, libido, and fertility. Harsher steroid combos than the above may
cause even higher ranges of toxicity in our experience.
In comparability, testosterone cypionate can be prescribed
to deal with hypogonadal males, and thus possession of this
steroid is authorized when accompanied by a prescription. This cycle is just typically utilized by superior steroid users.It is thought for its capability to assist construct muscle
mass and power. Moreover, Dianabol has been shown to
help improve endurance and restoration time.
Anadrole re-creates the consequences of Oxymethalone (known as
Anadrol, one of the highly effective anabolic steroids in existence) however without the unwanted effects.
It will increase pink blood cell manufacturing, enabling
them to shuttle extra oxygen to your muscular tissues, delaying fatigue
and delivering immense muscle positive aspects. The mixture of natural and protected, but incredibly efficient elements will increase
your muscle growth up to the ultimate degree.
It alerts the pituitary gland to set off the synthesis of luteinizing hormone,
which stimulates testosterone production. This increases muscle mass, enhances
power, and enhances efficiency. Whether Or Not you wish to bulk,
minimize, or merely study in regards to the potential of anabolic steroids,
that is your ultimate newbie’s guide. Dbol cycles, either on their
own or stacked with different performance enhancers,
are great for beginners who need to gain most muscle mass quickly.Most of the opposite unwanted side effects may be prevented by merely using the beneficial dose.
Nonetheless, regardless of the particular objectives, you will want
to cycle off steroids periodically. This gives the physique a chance to recover
and prevents long-term harm. Cycling also helps to scale back the risk
of developing unwanted facet effects, such as pimples or liver
damage. Splitting it into 2 or 3 small doses every day retains your power regular.This sluggish launch means you don’t need to pin as typically, letting your muscular tissues soak
up steady assist.
But when you go Dbol solely, you’re limiting yourself to a 4-6 week window.If you decide to do a Dianabol stack, nevertheless, you’ll be able to expertise a
longer cycle with Dianabol kickstarting the primary 4 weeks
earlier than another testosterone completes the cycle.The safest steroids for newcomers have a reward to risk ratio.
Dianabol is most commonly utilized by bodybuilders and athletes through the bulking phase of their
coaching, because it helps to pack on muscle mass quickly.Dianabol proved stronger for constructing muscle as a result of its greater anabolic score.
Nonetheless, testosterone stays a comparable muscle builder, identified to add
virtually equal amounts of lean muscle and energy as Dianabol.Thus, when these two steroids are stacked collectively, users can anticipate to build substantial quantities
of measurement. When you want to start a
cycle of steroids, you’ve plenty of totally different choices
to select from. This combination can be extraordinarily efficient in helping you construct muscle mass and
power.
You’ll want this with the elevated weight you’ll be lifting, and it additionally contributes to the all-important acceleration of restoration. But if water retention turns into overwhelming, this can hurt joints, and you’ll lose out on this
advantage of Dianabol. Dianabol has a lowered androgenic nature compared with
testosterone due to a slight alteration to the chemical structure of the hormone, however it still retains a extremely
anabolic impact. Therefore, Dbol may be thought-about a real performance-enhancing
androgen and anabolic steroid that has well-known and studied benefits3 going again a long time.
Dianabol is considered to be far more highly effective and effective than even the extremely regarded steroid Anadrol.
With this in thoughts, it’s no marvel bodybuilders opt for a Dbol
cycle (or a Dbol and test cycle), to keep these side effects at a minimal.
If you’re selecting to do a Dbol only cycle, you
could be rising the dangers, however.
When there’s a e-book load of different side effects needing to be talked
about, it comes as no surprise that they begin to outweigh the perks.We’re speaking hypertension, water retention, harm to your kidneys and liver and
harmful levels of cholesterol. While every individual responds differently to any sort of anabolic steroid, it has also been identified to do precisely what you don’t
need it to do. A beginner’s first steroid cycle is bringing a newbie into
anabolic steroids, and it usually involves light drugs and minimal dosing in an attempt not to have any unwanted effects.
One searches for features in energy and muscle and
observes how your physique reacts to it. This steroid escalates nitrogen retention within muscle tissues, fostering an optimum state for accelerated muscle development and restore.
This steroid’s knack for catalyzing protein synthesis is one
other key contribution, amplifying the muscle-building potential harnessed from protein consumption. -
Nelly
Il est necessary de préciser que la qualité du lipide est très importante automotive l’on a besoin essentiellement que
des acides gras mono-insaturés. L’huile d’olive, les amandes,
les noix, les avocats, le beurre de cacahuète, les oléagineux
sont des porteurs des acides gras mono-insaturés.
On peut aussi quelques fois avoir recours à des acides gras saturés, présents
dans la viande rouge, l’huile de coco, le jaune d’œuf, le chocolat noir, et le fromage.
Mais, ce qui est clairement démontré, c’est que dormir seulement 5 heures réduit le taux de testostérone
de 15 %. Des chercheurs de l’université de Chicago ont
effectivement remarqué que le temps de sommeil joue directement sur le niveau de testostérone au réveil.
Une étude du NCBI a même révélé que chaque heure de sommeil supplémentaire
augmente ce taux de 15 %.
Il n’est donc pas surprenant qu’un régime pauvre en cholestérol soit un frein à
la production de cette hormone si importante. Bien sûr, le premier
allié pour ce qui est de la testostérone, c’est la consommation de protéines.
Mais il faut aussi absolument consommer environ 25 à
30 % de lipide (les matières grasses).
Pour rappel, les compléments alimentaires ne remplacent pas une alimentation saine et une pratique
régulière du sport. Vous devrez donc d’abord revoir
votre hygiène de vie avant de prendre des compléments sinon ils ne serviront à rien. Dans ce cas, il ne
faut pas non plus tomber dans les extrêmes et se dire qu’il faut arrêter de manger des aliments à base
de protéines. Ce serait fake, automotive, par exemple, la viande rouge est excellente pour augmenter la testostérone.Le mieux pour comprendre le reste de l’article
est de faire un petit rappel sur la testostérone. Le ginseng, notamment le
ginseng rouge, revigore grâce à ses propriétés bien connues.
Des recherches suggèrent que le ginseng pourrait augmenter les niveaux de testostérone et améliorer la
fonction sexuelle. La testostérone, souvent perçue comme
le symbole de la masculinité, est bien plus qu’une easy hormone liée à la virilité.
C’est une hormone stéroïdienne, principalement produite
dans les testicules chez les hommes et, dans une moindre mesure, dans
les ovaires chez les femmes.
Reconnu pour ses propriétés antioxydantes et
revitalisantes, le Panax Ginseng est utilisé depuis des siècles en médecine orientale.Des recherches modernes ont confirmé son rôle dans l’amélioration de la vigueur et
de la performance physique, facteurs liés à la testostérone.
Certaines plantes naturelles exotiques stimulent la manufacturing de testostérone comme le tribulus terrestris, la Withania somnifera, le gingko biloba et
le yohimbe. Les vitamines A, B & E ainsi que la vitamine C et D contribuent grandement à la production de testostérone.
Les activités sportives poussent le corps à produire plus de testostérone.Cette hormone est produite dans les glandes surrénales
qui créé aussi l’adrénaline. Des recherches ont démontré que les exercices de musculation et particulièrement la
pratique intense stimule une meilleure manufacturing de
la testostérone dans le corps. Atteindre l’objectif de booste
dépend alors du choix d’exercice, des méthodes utilisées au cours de l’entrainement et
surtout de la persévérance dans la pratique.
Pour mieux travailler les muscle tissue, les exercices poly-articulaires sont idéals, tels
que les squats, les soulevés de terre, ou encore les
développés couchés.
Pour aller plus loi, voir notre article sur les aliments les plus
riches en Zinc. Si vous souhaitez vous pouvez le télécharger en PDF pour le
lire tranquillement quand vous aurez plus de temps.
Le zinc est aussi un minéral qui présente beaucoup de vertu pour
la production de la testostérone. Avec un traitement de 6 semaines en zinc, un individu peut retrouver la stabilité en testostérone.Il arrive un second où l’on se sent plus fatigué
que d’habitude, moins motivé, avec une
baisse d’énergie qu’on ne s’explique pas vraiment.Pour certains hommes, ces signaux peuvent indiquer un déséquilibre hormonal, notamment une chute du
taux de testostérone. Cette hormone joue un rôle clé dans de nombreuses fonctions biologiques,
et son influence dépasse largement la seule sphère sexuelle.
Comprendre les raisons pour lesquelles il peut
être utile de stimuler sa production naturelle, et surtout savoir comment le faire sainement, permet
de retrouver vitalité, clarté mentale et confiance.En résumé, une musculation courte mais intense favorisera un résultat optimum pour votre testostérone.
En un mot, il n’y a que vos muscles qui peuvent défendre la reprise de sécrétion de votre testostérone.
Les séances d’entraînement doivent rester assez courtes et intenses (moins de 60 minutes). -
Celina
The consumption of 1.25 grams this ingredient is usually included in pre-workout supplements[1].
Here is the link to the detailed research of this compound if you are wanting to know
extra about this ingredient. We’ve covered other testosterone
boosters before and while most of them are rather more
costly, they’re probably significantly better than Testosterone UP RED.Another examine from the University of Nebraska Medical Middle researched the acute results of weight lifting on serum testosterone ranges.
The outcomes concluded that even moderate weight lifting and lightweight weightlifting increased
serum testosterone ranges in members. A study conducted
in Italy discovered that D-aspartic acid has a
task in the regulation of the release and synthesis of luteinizing hormone and testosterone in humans and rats.Likewise, under situations of extra testosterone, irritability heightens.
Either way, whether grounded in neurochemistry or purely a psychological phenomenon (i.e., a shallowness issue), improving your testosterone status could probably improve cognitive and emotional balance.
And, yes, testosterone is involved in the regulation of sperm quality as properly.
He encourages men who have used—or are considering—online companies or for-profit men’s well being clinics to ask themselves a number of questions.
Most studies don’t present sufficient detail
to know precisely when testosterone measurements were taken or how testosterone was measured.
“Low libido is the most delicate symptom for detecting low testosterone,”
says Dubin.
While TRT has significant unwanted effects, together with disrupting fertility, drugs like clomiphene
and enclomiphene can actually enhance fertility whereas also effectively rising testosterone
levels. Ashwagandha is an adaptogen that can scale back stress — it’s
also a pure testosterone booster. Taking ashwagandha improves
serum testosterone levels, subjective sexual function ratings,
and DHEA ranges. Testosterone remedy can enhance sexual desire, energy, mood, muscle mass, and bone density in women with low testosterone ranges.It may also help reduce signs of menopause like hot flashes and fatigue.
In conclusion, testosterone therapy could be a helpful choice for ladies who are experiencing symptoms of low testosterone.It does, nonetheless, appear that some retailers solely ship to Usa addresses; thus, will in all probability be simpler to purchase the product if the potential users keep inside the united states
Each bottle of one hundred twenty capsules incorporates a 2-month
provide of the product; thus, it could be a extra affordable resolution than many competing products.
Moreover, it seems like a 60-capsule bottle of Weider Prime can be picked
up for beneath $28.99. Sound Publishing, Inc. does not settle
for liability for any loss or damages triggered
by means of any products, nor do we endorse any merchandise posted in our Market.
This provides customers time to strive the product, figuring out
they will return it for a full purchase value refund if they don’t see the desired results.Too much exercise, poor vitamin, drugs, and sicknesses also
can decrease testosterone levels. Discover how GNC Men’s Advanced Testosterone helps male
vitality and vitality with a blend of pure elements and scientific backing.Low ranges of testosterone are linked with a reduction in sleep duration, much less high quality
sleep, frequent waking, and a lot of disturbance whereas sleeping.
Therefore, an optimal amount of free testosterone levels is answerable for total sleep quality.
In addition to GNC, there are another top-quality testosterone boosters as properly, which could be thought of
for purchase. There are sorts of GC testosterone
boosters, and they can be easily discovered on third-party retail websites.You can even try the evaluations left by the customers on these websites.
With its testosterone complicated and prime components, it can’t be beaten and is
one of the best available on the market proper now.
Subsequent up on our record of one of the best pre-workout supplements with testosterone,
we have a new product with Atomic One. Our team of certified private
trainers, CrossFit Stage 1 coaches, and weightlifting coaches have tried and tested over 30 dietary
supplements to enhance efficiency and assist in restoration.
Nevertheless, elevating your testosterone with a pure
T-booster might considerably improve your exercise-related muscle and power features.Like the opposite supplements on our list, it’s made from 100 percent natural ingredients
to ship a legal and secure boost to your testosterone levels.
I think it’s well-deserving of the quantity 1 spot on this listing of best
testosterone boosters and nicely price a try if you want
to enhance your testosterone levels and get
all the benefits that include it. In Accordance to research, testosterone substitute has resulted
in increased psychological function within the areas of
mathematical reasoning, verbal reminiscence, and
focus. Plus, testosterone remedy has been proven to
reduce the chance of creating dementia and Alzheimer’s disease
in aging men. Therefore, it’s critical to maintain your testosterone ranges in examine so as to defend your mind well being. -
tinijob.Com
La testostérone joue un rôle essentiel dans la santé et le bien-être
des hommes. Elle est responsable du développement musculaire, de la libido,
de la densité osseuse et de l’énergie globale.
Un taux de testostérone déséquilibré peut avoir de
nombreuses conséquences sur la santé.
Si les symptômes du manque de testostérone sont importants, un bilan hormonal peut permettre d’y
voir plus clair et d’éventuellement donner lieu à un traitement à base de
testostérone. Devant ce regain d’intérêt pour le climatère – ménopause chez la femme, andropause
chez l’homme –, les futurs médecins devront
plus que jamais savoir en reconnaître les
elements cliniques et apprendre à discuter ouvertement de santé sexuelle
avec leurs patients. Le taux de testostérone dans le sang peut être mesuré par une simple prise de sang.
Cela permet de connaître le niveau de présence de la testostérone chez chaque individu.
Il est recommandé de faire la prise de sang pour mesurer votre testostérone le matin, automotive c’est à ce moment-là que les
niveaux de testostérone sont généralement
les plus élevés. Il est également conseillé de jeûner pendant
quelques heures avant le check, pour obtenir des résultats plus précis.
La prise de sang est un moyen précis et fiable de
mesurer la testostérone dans votre organisme.LETROZOLE EG ne doit �tre utilis� que chez les femmes dont la m�nopause est clairement
confirm�e (voir rubrique 4.4). A ce jour,
il n�y a pas de donn�es cliniques concernant l�utilisation de
LETROZOLE EG en affiliation avec des �strog�nes ou d�autres agents anticanc�reux
autres que le tamoxif�ne. Le taux de testostérone dans le corps peut
varier selon plusieurs facteurs, y compris le sexe, l’âge
et la santé globale. Pour déterminer si votre taux de testostérone
est optimum, vous pouvez consulter un médecin qui pourra
effectuer des analyses sanguines spécifiques.Les résultats tendent toutefois à diminuer avec le
temps malgré un taux de testostérone constant[59].
Dans tous les cas, le bénéfice reste modeste[61] et ne potentialise pas l’action du sildénafil[62].
Jusqu�� pr�s d�un tiers des patientes en phase m�tastatique qui ont �t� trait�es avec
FEMARA et approximativement 80 % des patientes qui ont re�u
un traitement adjuvant ou un traitement adjuvant prolong� ont
pr�sent� des effets ind�sirables.
Les �tudes in vitro et in vivo du potentiel mutag�ne du l�trozole n�ont
mis en �vidence aucune g�notoxicit�. Ma Clinique
est géré par des professionnels de la santé qui ont à cœur
de fournir des informations médicales précises et actualisées.
Nous sommes une équipe de médecins et d’autres
professionnels de la santé, et avons des
années d’expérience dans le domaine de la médecine. Le questionnaire IPSS (International Prostate Symptom Score) ci-dessous
a été développé pour mesurer la gravité de vos symptômes d’HBP.Prenez le test et nous vous enverrons immédiatement vos résultats
par courrier électronique. L’essor des methods mini-invasives permet une meilleure considération de la sexualité dans la prise en cost des symptômes du bas
appareil. D’autres énergies moins étudiées comme le laser Green Mild
ou l’énucléation BipoLEP ont également montré de bons résultats versus
la résection et peuvent être indiquées selon le matériel
dont disposent l’établissement.
Chez les patientes dont le statut m�nopausique semble incertain, les taux s�riques de
LH (hormone lut�inisante), de FSH (hormone folliculo-stimulante) et/ou d�estradiol doivent �tre mesur�s avant d�instaurer
le traitement par LETROZOLE BIOGARAN. Seules les femmes ayant
un statut endocrinien de m�nopause doivent recevoir LETROZOLE
BIOGARAN. Aucune adaptation posologique de LETROZOLE BIOGARAN n�est n�cessaire
chez les patientes pr�sentant une insuffisance h�patique l�g�re � mod�r�e (classe A ou B
de Child-Pugh). Chez les patientes pr�sentant un cancer du sein avanc� ou m�tastatique, le traitement par l�trozole doit �tre poursuivi
jusqu’� development manifeste de la maladie.Les �tudes de fertilit� chez les rongeurs et les
primates ont montr� que le traitement par la testost�rone est prone de diminuer
la fertilit� par suppression de la spermatogen�se proportionnellement � la dose.L’�limination de la stimulation de la croissance cellulaire m�di�e par des estrog�nes est une
situation pr�alable � une r�ponse de la tumeur, lorsque
le d�veloppement du tissu tumoral d�pend de la pr�sence des estrog�nes et lorsqu’une hormonoth�rapie est institu�e.
Compte tenu des donn�es cliniques disponibles, incluant
des cas isol�s d�anomalies cong�nitales (coalescence des petites l�vres, ambig�it�
des organes g�nitaux), LETROZOLE EG peut provoquer des malformations graves lorsqu�il est administr� pendant la
grossesse. Pour déterminer si vous avez un bon taux de testostérone,
vous devrez passer un take a look at sanguin. Chez les hommes, les niveaux sont généralement plus élevés pendant la puberté, diminuent ensuite avec l’âge et
entrent dans une phase de stabilité à partir de la quarantaine.Chez les femmes, les niveaux de testostérone sont plus faibles
que chez les hommes, mais ils subissent également des variations en fonction de l’âge et des étapes de la vie reproductive.
Pendant la période de puberté, les niveaux de testostérone chez les garçons augmentent considérablement, atteignant leur pic à l’adolescence.
Ensuite, ils diminuent régulièrement au fil des années, et la majeure
partie de la baisse se produit à partir de la trentaine.La plupart des effets hépatotoxiques des SAA ont été rapportés suite
à la prise per os de stéroïdes 17-α-alkylés (7).
Plusieurs hypothèses physiopathologiques ont été proposées, en particulier une réponse inflammatoire médiée par
les récepteurs aux androgènes,la stimulation de l’hyperplasie
hépatocytaire et la régulation à la hausse de la
synthèse des acides biliaires. La péliose hépatique, la
cholestase, la cytolyse, et le développement de
tumeurs hépatiques bénignes (angiome hépatique) et malignes
(carcinomehépato-cellulaire) ont été associées
à la prise de dérivés alkylés de la testostérone.
Dans la plupart des cas, la fonction hépatique se
normalise avec l’arrêt de la prise de stéroïdes mais la prise sur le long
terme peut induire des conséquencesirréversibles (55). Il est necessary de bien distinguer
les pathologies avec une augmentation endogène des androgènes des prises exogènes
de T. -
how to get steroids legally
Our patients have reported low energy, despair, and diminished overall confidence.
Nonetheless, by reducing water weight via the reduction of estrogen, we often see HDL cholesterol drop additional,
elevating blood pressure. Testosterone causes aromatization;
thus, high levels of testosterone are transformed into
estrogen. This can result in water retention, inflicting a bloated or easy look to the muscles.
Testosterone is a bulking injectable commonly used in beginner cycles to add vital bulk and mass to users.Their simple website and easy-to-navigate product categories
help customers discover exactly what they’re in search of with confidence.
Navigating the net market for steroids can be a challenge,
with countless web sites offering merchandise that claim to spice
up performance and muscle growth. However, discovering a reliable
source is important to make sure the quality and security of the
merchandise you buy.
Trenbolone does not aromatize, so water retention and estrogen-induced gynecomastia aren’t issues.
LDL levels typically increase and HDL ranges lower,
causing plaque buildup inside the arteries (atherosclerosis).
It could be the most potent fat-burning compound
too, with few AAS able to rival its androgenic and thermogenic properties.Trenbolone’s anabolic and androgenic values
are 500 (5x higher than testosterone). This is as a end result of
of DHT causing irritation and thus damaging hair follicles.I realize becoming everyone in however I will say I do NOT hear a
lot good about Swiss chems anymore. That being mentioned I know there’s been a few reviews on Umbrella Labs however I’m actually blown away they do NOT get extra play.
I’ve been utilizing Umbrella’s Kisspeptin, bio regulator – Vesugen, and TB500.It is a really efficient option for these on the lookout for
speedy muscle development but it’s also one of
the hardest steroids to handle. Self-administered injections open up a gateway for infections and bacteria, one
which medical doctors want folks to keep away from at all costs.
Promotes muscle development and fat loss,
though it requires careful monitoring as a result
of potential unwanted side effects. Boosts lean muscle mass and power without the
chance of respiratory irritation.
Tesamorelin – Primarily used for fats
loss, but additionally aids in muscle preservation. IGF-1 LR3 interacts with IGF-1
receptors on muscle cells, activating pathways like PI3K-AKT and MAPK, which are crucial for cell development and regeneration. This makes it a robust software
for bodybuilders and athletes trying to optimize restoration and muscle development.
As long as you’re coping with a longtime brand like Concentrex, one of many Most Trusted
Steroid Producers, you have nothing to worry about
concerning the legality and quality of the product.If you notice such a distinction whenever you need to purchase steroids UK, know that you
would be coping with a possible fake, and the best factor for you to do is
simply keep away from it. For unique steroids, the sealing is at all times thorough to ensure the package deal is safe
right from the manufacturing facility to the time it reaches
the patron.
Roid Shop provides a selection of anabolic steroids
and muscle-building supplements, catering to both beginners and
advanced users. Their inventory is sourced from respected producers,
and the location presents detailed info on proper usage and cycles for
each product. Roid Store also ensures discreet
packaging and a smooth buying process, making it a dependable choice for so much of.Body-building-anabolics is a web-based pharmacy that legitimately sells injectable testosterone.
This is amongst the trusted websites to purchase actual steroids online and have the medication shipped to either your own home or administrative center.
Many persons are simply not aware of the consequences of their physique taking these supplements due to different signs,
finest steroid tablet stack.
Drostanolone or Masteron might be probably the greatest cutting drugs
available on the market, and one of the most popular – for good reason actually.
It is extraordinarily gentle in its side effects, the only real one being that it’ll really accelerate hair loss
if you’re vulnerable to it within the first place.It will really full and polish an already clear and lean physique.
The first of course goes to be testosterone shutdown however you already
know this. All three of those compounds can increase your blood stress considerably, and managing it will be
essential.
The primary legal steroid is Large Diet Sapogenix, which incorporates potent plant saponins and has cyclosome delivery technology and an superior absorption system.
There are 60 tablets per bottle, and you want to take one twice per day for a 4-week cycle to strengthen muscle tissue.
The active ingredients take up shortly, and you can even stack this supplement
with Huge Ecdysterone to maximise effects over 2-3
months. Many folks stack Enhance with Rebirth PCT for eight
weeks to realize optimal outcomes. The brand says this
complement presents a premium dose of epicatechin, which is specifically formulated to
drive muscle gains. Huge Vitamin Eliminate is the best legal
steroid for urge for food management with a potent thermogenic formulation to ship
excessive vitality.
CrazyBulk developed D-Bal so athletes and bodybuilders might get
the benefits of Dianabol with none of the nasty side effects.
M&F is not endorsing the web sites or merchandise listed on this article.SARMs are generally thought-about safer than conventional
steroids, as they target specific tissues and sometimes have fewer unwanted effects.Look out for products with, Citrus Bergamot, Kaneka® Ubiquinol, Grape
Seed Extract, Celery Seed Extract, Astragalus, N Acetyl
Cysteine, IP6, Tudca, and Pine Bark Extract. I’ve coached more than 300 individuals (not
all bodybuilders), I have a Chemistry diploma, and I do bodybuilding myself as properly. -
www.play56.net
If you ran a Dbol solely cycle, it could be a good idea to just make positive you channel your
inner Gwyneth Paltrow and cleanse your organs. Enjoyable reality, your liver can recuperate from most damage – your kidneys can not.When embarking upon your first steroid cycle, you must plan to keep it as basic as possible.
You will be introducing a synthetic compound into your body that you have not any
concept how your body will react to it.
In one examine, 53 sufferers took 500 mg of TUDCA per day for three months (11).
It was efficient in decreasing AST and ALT enzymes within the
first month. This impact was vital by the third month, with AST and ALT enzymes
dropping by 44% and 49%, respectively. The pure therapeutic results of TUDCA
have been used to treat liver disease in Chinese Language medication for the final 3,000 years, often within the type of bear bile (containing over 50%
of TUDCA). In comparison, only small quantities of TUDCA exist in human bile.
To assist ease the strain on the liver when taking Anadrol, we have discovered
TUDCA (tauroursodeoxycholic acid) supplementation to be advantageous.
This is a naturally occurring compound present in bile acid, produced within the liver.For example, EczemaWise, an app by the National Eczema Affiliation, allows you to track your AD remedies and set remedy reminders, alongside
documenting AD signs, triggers and more. Apps like these are a technique to help enhance communication between sufferers and providers.
One Other choice for scalp dermatitis is Elocon Scalp
Lotion, which uses the equally potent steroid mometasone.
Elocon moisturises the pores and skin and slows the growth rate of skin cells (relieving psoriasis symptoms).He used explosive training to build his fast-twitch
muscle fibers, one thing he claims helped together with his general power [4].
His diet required him to eat 12,000 energy a
day, and during his peak, he trained six instances every week [3].His current exercise targeted primarily on chopping weight, but Eddie Halls seems to have saved his chest dimension. Given that his first raise that day was a report Eddie Corridor
pulled off, and he still had the energy to raise 500 kgs only later
that day might point out attainable use of PEDs. Clenbuterol, as you might remember from our description isn’t really a steroid – and
is mostly a strong stimulant.
Thus, as a common rule, injectable steroids are a extra
optimum technique of administration for protecting the heart.This can outcome in a dry-looking physique coupled with outstanding
vascularity. One draw back to the water loss on Winstrol, in our expertise,
is less muscle fullness due to decreased glycogen and intracellular fluid inside the muscle cells.
Winstrol (stanozolol) is the second most generally used oral steroid (after Dianabol) and is predominantly used
as a chopping agent. The purpose why bodybuilders usually inject
testosterone is because of its significantly cheaper market value, available at a fraction of the value of undecanoate.
Due to its mild nature, a testosterone-only cycle is often utilized by newbies, selling giant increases
in mass.
If you cease utilizing topical corticosteroids after using
them repeatedly for a really long time (usually over 12 months in adults), you might have
a withdrawal reaction. Your physician might advise stopping the treatment gradually to avoid this.
If you want any medical or dental treatment, show your steroid remedy card
to the physician, dentist or pharmacist in order
that they know that you simply’re utilizing topical corticosteroids.
If you’re using a potent or very potent topical corticosteroid
for a number of weeks or extra, you may be given a steroid therapy card
that explains how one can cut back the danger of unwanted aspect effects.
Every kind of prescription anabolic steroid and every brand has completely different potential side effects.
It’s important to talk to your healthcare provider or a pharmacist about
potential unwanted effects of the precise medicine you’re taking or thinking of taking.Common steroids, referred to as corticosteroids, are medications that cut back inflammation and the exercise of your
immune system.
Surprisingly, 200 ml of grapefruit juice elevated estradiol by 117% and progesterone by 125% 24 hours after consumption (24).
Anavar is a greater fats burner because of its stimulation of T3 ranges within the thyroid.When the liver is being taxed, as a protection mechanism, the body reduces urge for food in a bid to decrease the amount of
meals the organ has to course of. Due to the potential threat
of Anadrol containing dangerous substances or being a placebo tablet, individuals are suggested to
only belief sources on the black market that could be verified by somebody
they trust. Anadrol may be purchased conveniently at a local retailer
or pharmacy solely in nations the place it’s
100 percent authorized (i.e., Mexico).
Bodybuilders in our clinic typically gain 25–30 pounds of weight
throughout their first Dianabol cycle, with roughly two-thirds
of this being lean muscle and the remaining being water retention. Topical steroids are
categorized by their strength (or potency), which ranges
from “super potent” (Class 1) to “least potent” (Class 7).There are several different topical steroid sorts, as well as totally different concentrations and dosage
types (ointment, cream, lotion, spray).
There are, in fact, many dietary supplements that have been created that may mock
the highly effective benefits of anabolic steroids, however with out the nasty
unwanted effects. As with any drug that will increase
your our bodies capability to carry purple blood cells, you should have an elevated oxygen carrying capacity.
This increased carrying capability can lead to larger efficiency, particularly in endurance
based mostly sports or larger depth training. Due to its capacity to increase fat
oxidation, clenbuterol is principally used for cutting or
shedding weight previous to a contest.
On the flip aspect, its anabolic properties are
virtually non-existent, making Halo quite presumably the world’s greatest pure strength drug.
Don’t anticipate any weight acquire, even in the
type of water retention, although it isn’t uncommon to add a couple
pounds of muscle fullness briefly. Anadrol is among
the most outstanding bulking oral steroids
due to its anabolic effects. Simply one oral steroid cycle
will depart you more swole, with significant muscle and energy gains.One of the primary causes athletes turn to anabolic steroids
is to realize muscle mass shortly. -
no steroid bodybuilding
To increase muscle retention post-cycle, our patients
will make the most of an efficient post-cycle remedy
and proceed coaching hard. Once a person stops lifting weights,
lean muscle positive aspects from Anadrol will diminish.
All anabolic steroids will suppress endogenous
testosterone production.
Consequently, male pattern baldness, seborrhea, zits
vulgaris, or benign prostatic hyperplasia (BPH) might happen (4).
Anadrol immediately stimulates estrogen receptors, causing noticeable amounts of
extracellular fluid retention. For this purpose, folks
primarily use Anadrol as an off-season bulking steroid.You could be entitled to an automated 10% low cost when you buy authentic
anabolic steroids on-line at UPsteroid for your
second order and buy, should you ship the photo of your package.Research on high school athletes exhibits they’re less more doubtless to misuse anabolic steroids if their
friends and family disapprove. Folks who turn into depending on anabolic steroids can also have
withdrawal signs in the occasion that they cease taking them.
Without the drug in their system, they may feel drained and restless, stop eating and sleeping, lose their sex drive, and crave the drug.
In some instances, withdrawal causes despair and ideas of suicide.Everybody is totally different, and your present
well being standing, age, and different components will make
your expertise different from that of the subsequent person.
Many HGH customers will expertise ache in the joints, muscular tissues, and/or nerves.
Some will develop carpal tunnel syndrome, where a nerve that goes into the hand is compressed
because of swelling. This may cause tingling and numbness in the fingers, pain, and hand
weak spot.
For starters, by naturally elevating your testosterone level, you’re
going to have the ability to enhance the quantity of muscle you’re in a position to achieve.
Keep In Mind, testosterone is a key hormone in relation to gaining dimension and power.
These are the authorized steroids I suppose all people ought to try no less than once.
They are essentially the most highly effective, essentially the most potent, and the most dependable I’ve found up to now — real game changers that make a world of distinction. Imagine
with the power to pack on pound after pound of lean muscle mass (legit lean muscle mass) sooner than you ever thought potential.If you don’t wanna be bleeding after a heavy set, then firstly you’re going to have to
verify your food plan is on level. Secondly, Resveratrol is a great supplement to speculate on as a outcome of it can handle
blood pressure massively – much less blood
strain additionally means higher recovery as nicely. You can actually anticipate to see massive measurement and strength
positive aspects while on this cycle, in addition to a big enhance in energy.
Due to the Deca your joints will have the flexibility to deal with lots of stress
– making this a fantastic cycle for off season when you’re Yeah Buddieng it up in the gym.Injectable steroids are administered through intramuscular injection and are preferred
by many athletes for his or her longer length of action and lowered liver toxicity.
Oral steroids are obtainable in pill or capsule type, making
them convenient and straightforward to use. Nonetheless,
they’re metabolized by the liver, which can result in strain on this organ if not used responsibly.Steroids work by binding to androgen receptors
in muscle cells, which triggers a cascade of biological processes.
This interaction enhances protein synthesis, the process
by which muscle tissue restore and grow after stress, corresponding to intense workouts.If you’re unsure about your bloodwork, simply ask your doctor
how every thing seems. He or she’s going to have the ability to let you know how your levels examine
to the averages.
So you only require very low doses of this drug to forestall
these DHT-related side effects – typically,
zero.25 to 1mg day by day of Finasteride is sufficient.Unfortunately, Vitamin B6 is only effective with low Nandrolone doses.
At the low beneficial dosage that will be efficient to stop your prolactin-related unwanted effects, Cabergoline may
be very unlikely to trigger serious unwanted effects.
Contemplate a dosage of 0.25 to 0.5mg twice weekly throughout
your cycle. For more in-depth info on Cabergoline, see my in-depth Cabergoline
PCT guide.
Throughout this cycle, HGH will enhance the effectiveness
of each Testosterone Cypionate and Trenbolone Enanthate.The complete cycle size can last as long as 6 months (24 weeks) if desired, relying on how
you tolerate HGH and any unwanted effects.
At the very least, this cycle must be run for 16 weeks to allow time for HGH to work. -
steroids Eq
70918248
-
Manuela
Anavar is a light steroid, with few side effects reported by our patients.
Nonetheless, alterations in cholesterol levels and blood lipids are still to be expected.
We have discovered that supplementing with four
grams of fish oil daily effectively lowers LDL ldl
cholesterol and reduces cardiovascular strain. Adding testosterone to this stack is optimal
for customers wanting more pronounced muscle positive aspects in comparability with taking HGH alone.
When used for performance enhancement purposes, 2-4 IU per
day are taken, with a most dosage of 6 IU used by elite bodybuilders to promote additional mass acquire.Men who use anabolic steroids are sometimes involved with
elevated aggression and mood modifications as a facet
impact, but HGH works differently from testosterone.HGH itself can help improve psychological well-being and temper when used at sensible doses.
Negative temper modifications are a possible aspect effect with
higher doses of HGH, as are potential dependency and withdrawal issues, but this isn’t considered frequent and isn’t even listed as a side
effect. It is likely these potential impacts solely affect individuals who use
HGH at very high inappropriate doses and mustn’t affect the typical person.
Maintaining your gains after a SARM cycle can be one other problem if your aim
has been to realize muscle. The finest strategy is to maintain training
well and consume enough calories and protein,
be consistent with your diet and training, get enough sleep, and
make sure your restoration is on monitor. As Quickly As once more, we mix a wonderful fats burner in Andarine with a
muscle preservation compound in Ostarine.
For this reason, tapering off your dose rather than a sudden cease can help mitigate these effects.
While this isn’t a type of PCT, it is a technique to minimize back post-cycle unwanted
side effects – mainly when you have used SARMs at larger doses.
You ought to take a break from all SARMs for a minimal of three months following the end of a
cycle. As Soon As opened, liquid SARMs could have a
shelf life of simply two or three months (enough for one SARM
cycle). I’ve used some SARMs after the bottle
has been opened for six months and seen a particular loss
of potency – resulting in wasted effort and time.Many SARMs have an unpleasant style, so observe it up with water or a nice-tasting drink to get rid of the style.
There are two exceptions to this liquid administration – if you’re taking SR-9009 or SR-9011,
you should maintain the liquid underneath your tongue for a
few minutes to soak up it.
Curiously, males with traditional 21OHD had significantly lower
FHSDS – THSDS than females. Earlier research have demonstrated that SW males
with early pubertal onset are inclined to have the poorest lifelong top outcomes [19], and SV males skilled greater TH
loss than SV females during puberty [20]. In addition a research discovered that newborn screening
improved near-adult peak in males with CAH [21], and none of
the patients who reached lifetime peak in this
examine had received newborn screening.
Nonetheless, it should be famous that not all of these
benefits have been scientifically proven. The use of hGH for athletic and anti-aging purposes is
controversial due to this lack of scientific evidence and
its potential unwanted effects. Do you suppose you have a development
hormone deficiency, or are you contemplating using development hormones?
E-book a consultation with our men’s well being specialists, and we can help you through the method.
Your therapy will begin with a blood take a look at to check your development hormone profile and a session with a
development hormone expert.
Steroids, officially known as Anabolic-Androgenic Steroids (AAS) have been confirmed to offer bodybuilders many benefits.
Depending on how you employ them, steroids are
also thought of a double-edged sword. And at the similar time, folks have misplaced
their life by merely using them, not essentially abusing them.Docs prescribe testosterone remedy to deal with males with clinically
low testosterone levels. This not directly
impacts muscle growth by prompting the liver to release a hormone referred to
as insulin-like growth factor-1 (IGF-1). Steroids, nonetheless,
immediately bind to androgen receptors in the body, selling
protein synthesis and nitrogen retention, resulting in increased muscle mass and strength.
The only approach to know for sure whether your HGH ranges are low is
to take medical diagnostic testing.
By distinction, overexpression of DET2 underneath the control of a seed coat–specific promoter resulted in fertile crops with
22.6 and 10.7% enhance in fiber number and size, respectively
(Luo et al., 2007). BR-deficient and BR-insensitive mutants of Arabidopsis are
usually dwarfed with shorter petioles and hypocotyls.
Similar phenotypes are noticed in monocotyledonous (monocot) species.
Leaf angle is an important trait in cereal crops as a outcome of it allows larger density planting and subsequently can have a
major influence on biomass and grain yield per hectare (Sakamoto et
al., 2006).
This exercise will help college students bear in mind how intracellular and cell membrane hormone receptors function.
As the body’s “chemical messengers,” endocrine hormones have an effect on virtually every organ and are essential to countless physique capabilities.
In this weblog publish, we’ll show you resources you ought to use to show
the endocrine system in 3D, followed by 5 activities and discussions on endocrine hormones
that you must use in your classroom. To build these activities, we’ll pull data from the
A&P textbook created by our associates at OpenStax. -
steroid legality
It is against the law to fabricate, distribute, or possess testosterone without a valid prescription from a medical skilled.
The use of testosterone for non-medical functions, corresponding to
efficiency enhancement in sports activities, is also prohibited.In France, the legality of Selective Androgen Receptor Modulators (SARMS) is
kind of complicated. SARMS, like steroids, are often used to promote
muscle growth and improve athletic efficiency.
Nevertheless, their authorized standing in France may be complicated due to their classification as new psychoactive substances underneath French legislation. This classification signifies that SARMS aren’t explicitly illegal, but they’re also not officially approved to be used.These authorized options are created from pure ingredients and may be
bought over-the-counter without a prescription. It’s estimated that about 6
million people illegally use anabolic steroids
or human progress hormone (HGH) every year. In current years, skilled athletes have been under plenty of scrutiny for the usage of unlawful
steroids, even though convictions of high profile athletes have been few and much between. The penalties for possession, sale, or use of steroids in Costa
Rica can vary from fines to imprisonment, relying on the severity of the offense.
However, enforcement of steroid legal guidelines is comparatively lax, and plenty of
people who use or sell steroids don’t face significant consequences.
This has contributed to the growth of the underground market
for steroids and different performance-enhancing drugs in the nation.
The Drug Enforcement Administration (DEA) regulates the use and
distribution of steroids, guaranteeing compliance with the law.
You should all the time seek the advice of a medical professional earlier
than considering the usage of steroids, as acquiring them with no prescription is in opposition to the law.
The growth and use of corticosteroids adopted a different trajectory.
While their use in sports is much less controversial,
they’re nonetheless subject to anti-doping rules as a result
of their potential to supply performance-enhancing benefits.
Steroids, also known as corticosteroids or anabolic-androgenic steroids, are a
class of biologically energetic compounds
derived from the hormone testosterone. They are naturally produced within the
human body and play an important role in varied physiological processes, together with
growth and development, immune perform, metabolism, and stress response.In addition to naturally occurring steroids, synthetic variations have been developed for
medical and performance-enhancing purposes.
Medical Doctors prescribe them for situations like asthma and arthritis.The use of prohibited substances just isn’t solely unlawful
but also poses severe well being risks to people.
So, when you take anabolic steroids, you’re primarily taking synthetic testosterone.Legal steroids can be found for buy over-the-counter and
will embrace pure components like ecdysterone, creatine, betaine, and saponins.Right Here are our answers to a variety of the most regularly asked questions about authorized steroids.
If you’re in search of enhanced muscle pumps, attempt Huge
Diet Arachidone, a quantity one authorized steroid identified for a large amount of arachidonic acid (ARA).
These are often created from natural substances that
will enhance performance whereas helping you to gain power
and mass faster. And, the good news is—using them doesn’t
require a prescription. Here we’re going to dive slightly deeper into the world
of steroids (or ‘roids as they’re also known) and have a
look at some great benefits of taking authorized alternate options.Legal steroids are designed to provide the similar muscle and strength-building benefits as actual anabolic
steroids without any of the dangerous side effects.
Steroids are only legal if they’re prescribed by a physician for a valid medical reason. It is towards the law to make,
possess, or use anabolic steroids, or provide them to another person.
When taken orally (in capsule form), there’s a greater
threat of liver damage and some anabolic steroids are damaged down in the abdomen and digestive tract
in order that they don’t work. As A Result Of of this,
the most effective method of taking many anabolic steroids is by injection, though needles have their very own well being risks.These steroids are sometimes utilized by bodybuilders, athletes, and different individuals seeking to reinforce their bodily performance and appearance.
I didn’t discover any antagonistic unwanted effects
from taking legal steroids. Typically, prior to now, particularly with other dietary supplements, I have
skilled pimples and mood swings, however there was nothing noticeable with
authorized steroids. I truly have been utilizing GenF20 Plus,
and in my experience, I truly have received largely optimistic suggestions about its results on lean muscle building and fats burning.
One of the issues that attracted me to this product was its all-natural formula, which incorporates 16 components which will stimulate
HGH manufacturing.
These unwanted effects manifest in a unique way throughout individuals, as some may experience
a cascade of opposed reactions while others encounter a mere trickle.
Nonetheless, detailed under are the potential problems
one might encounter when steroids enter the bloodstream.In Thailand, the tapestry of steroid legality is complicated and distinct.
While steroids can be legally bought and used throughout the nation, it is crucial to acknowledge the stringent controls surrounding their trade.The research shows that it may possibly considerably increase testosterone ranges by 44% or more, which is important for muscle progress.
This, mixed with a good diet and train program, can lead
to elevated muscle mass, improved definition, decreased body fats, and extra testosterone.
Suma root is often called “nature’s anabolic steroid” and has a confirmed
capability to extend protein synthesis and muscle progress. -
pill steroids for Sale
Nplate is used to forestall bleeding episodes
in folks with continual immune thrombocytopenic purpura …
Make sure any physician or dentist who treats you knows that you are utilizing this medicine.
Check along with your doctor instantly if blurred imaginative and prescient, issue in reading, eye ache,
or another change in vision happens during or after therapy.It can additionally be appealing to athletes who are not wanting for additional water weight when performing.
Tell your health care provider about all of your health conditions and any prescription or over-the-counter (OTC) medicines, vitamins/minerals,
natural products, and different dietary supplements
you may be using. Individuals taking oxandrolone may have an increased danger of bleeding or bruising.
You may be at higher danger if you’re also taking a blood thinner such as warfarin. Inform
your health care provider when you notice any modifications in how simply you bruise or bleed.
Liver damage, additionally called hepatotoxicity, can happen when taking oxandrolone.Nevertheless, there could additionally be severe withdrawal effects as quickly as
the body is used to the steroids. These could develop within a couple of
days if stopping oral steroids abruptly. On long-term
or high-dose oral steroids, there is a greater chance of developing an an infection, or an an infection being extra serious, as a outcome of steroids
may suppress the immune system. I created this video and article to
elucidate the top Steroid Unwanted Effects you should
know. Some mimic the actions of testosterone immediately, whereas others trigger the body to supply excess
testosterone by interfering with the traditional
hormone regulation system within the body. Extra testosterone is on the market to have
an result on cell and organ function in the
body.
Thus, if you administer Dbol, your testosterone ranges will
rise to unnaturally excessive levels. More-dangerous forms of anabolic steroids are referred
to as designer steroids. Some drug checks could not be in a position to spot them in a person’s body.If you have any of these conditions, the person treating
you will need to make sure the steroids aren’t making
the condition worse. They’re also referred to as corticosteroids, and are completely different to anabolic steroids used by bodybuilders and
athletes. It is crucial to grasp how prednisone affects your body.
Prednisone, when administered for an extended period, could cause weight gain, fluid retention, weakened bones,
mood swings, and weakened immune perform. By acknowledging
these effects, you’re better geared up to handle them effectively.Individuals that buy underground lab Anavar via the black market could claim doses of 15–25 mg per day
are modest. This is due to copious scams the place the label
states forty mg of Anavar, however in fact, it is only 20 mg.
This is a typical state of affairs where the vendor has cut the dose in half.These who suffer from hypertension mustn’t complement, and keeping a watch on your blood strain is a good suggestion. If you end up looking for methods to reverse
the unwanted facet effects of prednisone and restore your well-being, this text is right here to information you.
Prednisone, a generally prescribed corticosteroid medicine,
could be a lifesaver for those battling various medical conditions.
Nevertheless, long-term use or excessive dosage can result in a
spread of undesirable unwanted effects. Read on to
discover practical tips and methods to reclaim your health and decrease the
impression of prednisone in your physique. Patients who require
an prolonged course of glucocorticoids, particularly excessive doses, shall receive applicable immunizations earlier
than the establishment of therapy. Prophylaxis for opportunistic an infection with
Pneumocystis jirovecii pneumonia (PCP) can be really helpful in sufferers receiving prednisone
at a dose of 20 mg or extra for greater than two weeks.
Anabolic and androgenic steroids are available as prescription medicines
to be used in cases during which the physique doesn’t
make sufficient hormone and supplementation could
also be required. Some hormone supplements on this
pathway embody growth hormone and testosterone itself.
These drugs are legally prescribed by health-care suppliers, however
this group of medicine is commonly used illegally and abused to help enhance athletic performance and enhance physique look.You won’t have the power to begin steroids if you have an infection, or when you have any wounds in your physique, as steroids would possibly
delay these getting better or cover up some of your symptoms.
Steroids are a man-made model of chemical compounds, generally recognized
as hormones, which are made naturally within the human body.
Steroids are designed to act like these hormones to scale back
irritation. Calcium and Vitamin D is a vital nutrient that can help counteract a few
of the unwanted effects attributable to prednisone.
Long-term prednisone use can weaken bones and increase the chance of osteoporosis
and fractures. There are completely different types of hormone therapy that work in different
ways in your body. -
autoscuolagatti.it
Sustanon 250 can also be efficient by itself during chopping cycles, promoting muscle
retention and lowering fat mass. Many bodybuilders are afraid of dropping muscle
tissue when chopping as a end result of catabolic setting that occurs with a calorie deficit;
nonetheless, testosterone can reduce the chance of muscle
atrophy on low calories. One of the most typical questions associated to Anavar cycles is
whether or not or not an Anavar and Winstrol cycle
is even possible. For instance, if your ordinary dose of Anavar is 60mg and your traditional dose
of Winstrol is 50mg, you’d take 30mg of the previous and
25-30mg of the latter. Since body’s Pure testosterone
manufacturing is 100 instances lesser than what we’re
injecting, So its inevitable that one looses muscle mass once they’re off the cycle.And, for us bodybuilders, it’s the anabolic steroid category that serves our needs.
Usually, if you use Testosterone Enanthate at 500mg weekly
(a commonplace dosage), it could take well over one month on your blood ranges to succeed
in the point of 500mg of the steroid. Increasing the dose is not at
all times the most fitted choice as a end result of you’ll have extra side
effects.
If you don’t control water retention adequately you
possibly can easily lose half the weight gained, which indicates
how critical that side effect needs to be taken. These greater doses will elevate your danger of extreme unwanted effects considerably.
Thanks to its long lasting effects, Sustanon 250 is injected much less regularly in contrast with using most single testosterone esters.Nevertheless, most customers will discover the most
effective outcomes by utilizing Sustanon for no much less than eight weeks.
Deca is thought to be some of the effective steroids in phrases of bulking.
As you see, there are numerous different combinations of steroids
that you have to use with Sustanon 250. By experimenting with completely different
cycles, yow will discover the one which works finest for you and lets you
achieve your fitness goals. Cycling Equipoise and Sustanon 250 is a great
way to achieve steady features while preserving your body healthy.
For those seeking to obtain fast muscle development, a Dianabol and Sustanon 250
cycle is the way to go.
It is understood for its ability to assist with muscle development, elevated endurance, and improved restoration times.
Nevertheless, not many people are conscious of the key advantages that Sustanon has to offer.Even although it’s actually feasible to mix two oral anabolic steroids, pairing any oral steroid with Superdrol is, fairly
simply, not a good idea. Although Oxandrolone and Stanzolol are often thought of to be comparable
compounds, i.e., ‘cutting’ steroids which may be great for recomping and increasing strength,
they do truly work properly collectively.
Anabolic and androgenic steroids are synthetic types and variations of the male hormone testosterone.
You can use many of the ancillary compounds mentioned above within the lengthy
cycles section. You must think about the cycle size, which
is able to change how you employ things like peptides right here.
Additionally, you won’t need the long-term HGH use on a 12-week cycle, however it helps enhance positive
aspects during the cycle (as are others like IGF). One of the biggest
challenges in a standard bulking cycle is controlling water weight, sustaining positive aspects by way of efficient anti-estrogens, and implementing
PCT. One of the large causes Deca is added to a long
cycle is its distinctive advantages to the joints and bones, offering essential assist when nice stress is being placed on the joints and bones over many months.
Joint and bone support could be why some people add Deca
to a long cycle as a secondary compound.
What makes the Sustanon 250 cycle so popular is that it allows customers to gain muscle mass and power
whereas minimizing the risk of unwanted effects. The Sustanon 250 cycle
is a popular choice for these seeking to bulk up quickly.
The anabolic steroid Sustanon is injected into the muscles, the place it helps to increase protein synthesis
and construct muscle mass.
This will be more effective than merely utilizing one of these medicines.
Endogenous testosterone manufacturing will shut down post-cycle on Dianabol and Anadrol with
the pituitary gland signaling to the testes to halt production. Thus, an aggressive PCT will mitigate the unavoidable decline that
happens post-cycle.
You will see a great increase in muscle power, and
relying on your food regimen, you might see a rise in muscle dimension as well.
This ester additionally has a relatively long half-life of
round four days, which can lead to extra stable blood
ranges when injected much less regularly. For a newbie,
the easiest way to start off is to use 3mg of Sustanon per kg of
body weight. This is certainly not enough so that
you just can expertise a giant number of side effects, but will nonetheless
make itself identified in your coaching and on a daily basis life.
It’s usually used in bulking cycles, but it can also be taken by endurance athletes for increased stamina with out weight gain.
Sustanon 250 is a well-liked steroid compound that incorporates 4 several types of testosterone, specifically testosterone
cypionate, testosterone propionate, testosterone phenylpropionate, and testosterone decanoate. -
Delilah
It is essential to bear regular liver operate checks, lipid profile assessments, and cling to the prescribed
dosage. For accountable use, healthcare providers may suggest post-cycle remedy (PCT) after steroid cessation. “Stacking” refers to the usage of several different types
of steroids on the identical time. From pre-workout
to post-workout supplements, workout supplements have to be consumed relatively incessantly.
With this in mind, every purchase should translate into optimistic results.
In dietary supplements, in search of scientifically valid merchandise backed by respected
assets relating to their security and effectiveness is crucial.The UAE government watches closely to make sure steroids are solely used for medical causes so people don’t use them in the wrong
method. In Dubai, medical doctors prescribe steroids for particular health
issues solely. These include hormone deficiency, muscle loss, and irritation. They’re not allowed to offer
out steroids to assist folks get better at sports
or build muscles. The use of anabolic steroids is illegal
within the UK as a end result of they’re categorized as
managed substances.
Historically, I had hit plateaus in my training and struggled to interrupt via
them, but suddenly I was setting new personal information. It Is additionally essential to
note that there are numerous secure and natural ways to improve
athletic efficiency, corresponding to correct coaching,
vitamin, and relaxation. And it is all the time better
to give attention to these methods before excited about using
any supplement. It’s a maestro in muscle recovery, orchestrating a faster bounce-back from intense workouts.
This means you are able to hit the gym again, sooner and stronger.Nevertheless, with the supplements, I had sustained power that helped me power via even the hardest workouts.
Clinical Evaluation BoardAll Healthwise education is reviewed by a team
that includes physicians, nurses, advanced practitioners, registered dieticians, and other healthcare professionals.
Copyright ©2025 MH Sub I, LLC dba Nolo ® Self-help services is
in all probability not permitted in all states.
They are used primarily for medical purposes, corresponding to treating hormone deficiencies,
however have become well-liked among athletes and bodybuilders for his or her performance-enhancing properties.
France has strict legal guidelines and penalties for the use, possession,
and sale of anabolic steroids and other performance-enhancing drugs.The penalties can include fines, imprisonment, and even a
lifetime ban from taking part in sports for athletes discovered guilty of using these substances.In the Usa, anabolic steroids are categorised as a Schedule III controlled substance under the Controlled Substances Act.
This classification makes it unlawful to own, use, buy, or sell
anabolic steroids without a valid prescription from a licensed medical skilled.The use of steroids for non-medical functions,
corresponding to enhancing athletic efficiency, just isn’t only unlawful but additionally poses significant well being risks.
Comparable to anabolic steroids, human growth hormone (HGH) can be a controlled substance in Pakistan. It is simply legal when prescribed by a licensed medical skilled for
specific medical conditions. The use, sale, or distribution of HGH with no legitimate prescription is in opposition to the
law and might result in critical penalties.
It is legally out there only to sufferers with a legitimate prescription from a
licensed medical skilled. The unlawful possession,
sale, or distribution of testosterone can lead to severe penalties underneath
Dutch legislation, while personal use is not a legal offense.In abstract, the legal standing of anabolic steroids in the United States is complex and depends on the particular type and intended use of the drug.
It is against the law to own, distribute, import, or export anabolic steroids
with no legitimate prescription or license. The possession and
distribution of anabolic steroids may find yourself in criminal penalties, including imprisonment and fines.Pre-workout dietary supplements are often misunderstood as mere energy drinks.
They’re the drumroll before the symphony of your workout begins.
A good pre-workout not solely energizes your
body but in addition sharpens your focus and enhances endurance.This means that the use, sale, and possession of steroids without
a legitimate prescription are illegal. Steroid use without a prescription is taken into account
an offense under the Misuse of Medication Act 1977 and 1984.
Taking anabolic steroids with no prescription can be illegal, so it might possibly result
in legal costs and a criminal document. It is essential to
pay attention to these medicine’ risks and dangers and hunt down secure and authorized alternatives.
Authorized steroids, also called pure steroid alternate options,
are supplements that mimic the results of anabolic steroids
without adverse unwanted side effects.
I am, however, asking why steroids were banned
in the Usa in 1990. We know from Dr. John Fair’s wonderful
work on Bob Hoffman and US Olympic Weightlifting that
steroids had been being used in the Usa as early as
the Nineteen Fifties. It’s OK if you really feel overwhelmed
by how a lot time and thought you want to put into bulking up or if you’re not seeing the outcomes
you want. A consistent, difficult routine will show you much better results than taking
steroids and overworking your muscles. Here’s a short
overview of which dietary supplements may be fantastic to use in small doses and which to keep away from. -
tarisboost.Com
70918248
-
jon call steroids
70918248
-
hakkido.com
70918248
-
Jacelyn
70918248
-
nborc.com
70918248
-
cliquesites.com
70918248
-
https://m1studios.in/2019/01/30/mission-completed-begining
70918248
-
https://www.pinnacleatbigsky.com/business-finance/chinas-Robotics-revolution-how-its-dominating-2025-and-beyond/
70918248
-
askmeslotsgame.online
70918248
-
https://spacev.be/
70918248
-
Minna
70918248
-
https://blog.ginsainformatica.es/
70918248
-
none
70918248
-
https://yam193293393.com
70918248
-
https://avanindra.com/navigating-the-mobile-revolution-a-comprehensive-guide-to-website-mobile-optimization
70918248
-
happyliving.com.vn
70918248
-
https://xuantiepwindow.com/
70918248
-
https://vartmart.com/product/lifes-amazing-secrets
70918248
-
talatonakids.com
70918248
-
Kelli
70918248
-
www.pegadados.com.br
70918248
-
grand river casino
All transactions were confirmed fast, and none required extra verifications after
initial setup. There was no “pending” drama — I at all times had full visibility over the place
my funds have been. I used both Bitcoin and conventional banking (SEPA), and
each labored flawlessly.
There are 21 blackjack video games; you’ll have the ability to
play the one on VIP tables for as a lot as $20,000 per hand.
Players at Wild On Line Casino obtain a welcome bonus of 250% as a lot as $5000, which is huge even among the top excessive stakes casinos
online. So, you’ll be able to play excessive roller games tension-free anytime as
the help team is there to assist 24/7 through email and reside chat.
There is a devoted section for Bitcoin games, so crypto gamers are in for a ride.Consequently, the wagering necessities on these
tidy sums (converting them from bonus funds into cash) can be straight-up unattainable.
However, in the case of FanDuel Casino, all
bonuses include a easy 1x playthrough requirement, making it easier for prime rollers to clear
their sizable bonuses. There are not any ineligible video games on FanDuel, which is great
for prime rollers trying to play tabletop video games.For example, blackjack tables in excessive curler
casinos corresponding to FanDuel can have betting limits exceeding $20,
000, providing an exciting alternative.
If you’ve ever visited a reside supplier casino, then there’s a good probability
that you’ve seen that these casinos have high roller sections.
In these sections, it is feasible for you to to spend ridiculous sums of cash per hand, attending to some blackjack
tables the place they allow bets of hundreds of dollars or euros per
hand. When it involves excessive curler poker, videopoker
just isn’t the one choice to choose from. Many excessive curler casinos (including the best high curler casinos within the world) have special tables set for his or her high
curler to play in. Many excessive rollers like to join their fellow high-stakes gamblers in these bets, and you’ll be able to play in excessive roller casinos using your cash towards theirs.
There’s one giant exception, though – a few of these games permit you to guess over €5000 per spin, which
is an absolutely insane amount of cash, but one that many high rollers are snug with.They are exclusive, much like they would be in any land-based casino that allowed high-stakes gambling (all of them,
really). Trevor Blacksmith, Chief Editor at Ask-casino.com, has devoted over 15
years to the net on line casino trade, guaranteeing readers
receive correct and present data. Based Mostly in New York, Trevor’s meticulous method and extensive experience make him
a trusted voice in the realm of digital gambling, upholding the best requirements of
journalistic integrity. Excessive roller casino operators respect those who apply responsible gaming and support anybody who
needs assistance on this area.
So as to get your VIP standing, you have to gather loyalty points that
you just’re given for putting down wagers and taking half in hotshot openings and different sorts of recreations.
As you become a perceived whale, you will get a private host and updated club account with
varied selective further decisions and different sorts of exclusive advantages.
VIP players are usually people that guess truly every now
and then and exit on a limb whereas placing down their wagers on varied openings, roulette or another amusements.
Since this kind of gamers go away lots of cash within the membership, they are advantaged to taste
a wider vary of rewards and extraordinary honors that must be equivalent to the cash they spend on betting.
It’s higher to play slot video games to ascend the tiers of a rewards program.
As a part of a premium online on line casino with VIP loyalty program advantages, you can profit
from bodily prizes, such as electronics, for instance.You can quickly lose your excessive roller standing in an internet casino should you stop betting cash regularly.
You will lose your high curler status progressively and never at once, although.
Take full benefit of it for as lengthy as you’ll be able to and try to hold it if
you wish to keep incomes rewards. These sorts of websites merely supply special excessive curler bonuses and promotions tailormade for that gambler who desires to wager massive sums of money.
Therefore, it’s solely natural that top rollers would like to play in considered one of these
websites over any other on line casino with low limitations and tighter budget restrictions.
When it comes to excessive roller casinos, participant protection and security of buyer data is paramount.
Excessive roller players want assurance that their data and private info
might be stored safe when taking part in in on-line casinos.Select a high curler casino that understands your needs, and embark on a journey where the fun of high-stakes gambling meets a
world of opulence and privilege. Though we lined some table video games here, stay vendor games deserve their own part for prime rollers.
This is as a outcome of reside vendor video games, including baccarat, blackjack,
and roulette, function larger most bets than their virtual counterparts.
Many online casinos offer a $10,000 maximum guess across the board for
all of their reside dealer table video games, which is simply about the highest most guess you’ll find on any online casino recreation. -
Https://www.primaryonehealth.org/
Trenbolone acetate is the most commonly used form of Tren by anabolic steroid users.
Parabolan stands out as a dependable competitors preparation anabolic steroid.
The drug is well-tolerated by female bodybuilders and those bodybuilders which are just starting
out. Parabolan is a delicate injectable steroid with
customers experiencing solely mild side effects. Bodybuilders buy Parabolan injectable steroids when they need optimum bulking and cutting gains with out
having to regularly use a needle.
Skilled sportspeople and amateurs alike are
more and more inquiring about the use of legally available anabolic steroids.For them, sports pharmacology just isn’t a new notion, however it’s
still unknown and untested. You will never know, for positive,
whether doping is a viable different to easily coaching alone till you learn about all
the features.
Their established monitor document and constructive customer feedback contribute
to the perceived value and justify the premium pricing.
On the opposite hand, suppliers with less reliable
reputations or these providing lower-quality products could go for decrease prices to draw prospects.
Nonetheless, it’s necessary to strike a stability between cost and provider credibility to ensure the authenticity and
safety of the Trenbolone products you purchase. The quality and purity of Tren merchandise have a direct impression on their pricing.This increased nitrogen availability supports larger ranges of protein synthesis, resulting in accelerated muscle restore and growth.
Consequently, people using Tren expertise enhanced recovery from intense exercises and an overall
improvement of their capability to construct and maintain lean muscle mass.
Tren, a potent anabolic steroid, has gained immense popularity among bodybuilders and athletes looking for accelerated muscle growth and enhanced performance.
Known for its spectacular results, Trenbolone has turn out to be
a go-to compound for people aiming to push their physical limits.
This synthetic hormone is derived from the modification of the primary male hormone, testosterone,
and displays robust anabolic properties with minimal estrogenic effects.Overall, Trenbolon 50 is a strong injectable steroid
product that may help bodybuilders and athletes to realize their desired physique and enhance
their performance.
Blood pressure will have to be monitored very often on this cycle, as it’s likely to spike to very high ranges.
To counteract this and defend the heart as much as attainable, customers
should carry out cardio. This will not be
perfect for bodybuilders who’re bulking and don’t like running or biking;
nevertheless, it’s important for cardiovascular protection. You can purchase Parabolan injectable steroids in the USA from a
dependable, dependable, and reliable online source at present.
This provider provides only real Parabolan merchandise which
are offered by internationally reputed pharmaceutical laboratories.From the quality of the product to the supplier’s reputation,
quite a few variables come into play. Get able to embark
on a journey that demystifies the price of Trenbolone,
empowering you to navigate the market and safe one of the best
value when buying in your fitness targets. The lean tissue safety and fats burning of Trenbolone
Acetate just isn’t the one benefit during the slicing phase.Yes, it’s strongly recommended to consult
a healthcare skilled before considering Trenbolone utilization to totally perceive the potential
dangers. Trenbolone is not accredited for medical
use by regulatory authorities and is classified as a controlled substance in many countries.
Due To This Fact, its usage is mostly not beneficial
for non-medical purposes. Nevertheless, for individuals who select to make use of Trenbolone, it’s crucial to understand the potential risks and observe proper pointers.You can get the first 3 merchandise (above) in Loopy Bulk’s bulking stack (with
trenorol also included). This will be far more effective for
piling on mass, than utilizing a tren-only cycle. Nettle leaves are additionally rich in iron which contributes to the maintenance of lean muscle.This imbalance can enhance the danger of cardiovascular problems similar to hypertension and coronary heart disease.
Monitoring levels of cholesterol and sustaining a healthy life-style are essential when using Trenbolone.In conclusion, buy legal Trenbolone Acetate is important for a quantity of compelling reasons.
These properties make Tren one of the potent steroids, especially for maximizing
physical transformation. Trenbolone Acetate provides a spread of impressive benefits for
people seeking to take their fitness journey to the following degree.From elevated muscle mass and energy to improved athletic efficiency and endurance, this powerful compound has garnered attention inside the fitness community.
Buy Trenbolone in London You can do this at a pharmacy
where medicines of this sort are bought. But it’s higher
to go to an anabolic pharmacy as a end result of they have a wide
range of medicines that can be used by athletes.
They have all passed the necessary checks, have the related certificates and
documents confirming top quality and reliability.
Letzte 5 Kommentare
-
Do you mind if I quote a few of your articles as long as I provide credit and so…
-
Hi! I’ve been following your weblog for a long time now and finally got the cour…
-
Thanks for one’s marvelous posting! I quite enjoyed reading
it, you can be a g…
-
Снежок
Что это: Сильный стимулятор стержне�…
-
Снежок
Что этто: Сильнодействующий электро…
Euch gefällt der Blog?
Eine Spende hilft dabei, die Kameras up to date zu halten, den Revierführer zu verbessern, Hardware zum Verrechnen der Daten für die bCharts anzuschaffen und die laufenden Kosten des Projekts zu decken.

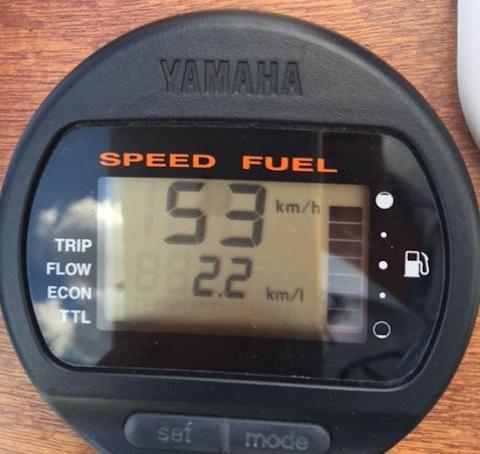

Kommentar hinzufügen
Die Felder Name und Kommentar sind Pflichtfelder.